【题目】已知:抛物线![]() 经过坐标原点,且当
经过坐标原点,且当![]() 时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
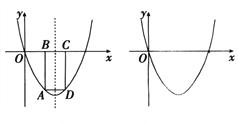
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB![]() x轴于点B, DC
x轴于点B, DC![]() x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①6 ,②L=
;(2)①6 ,②L= ,当A的坐标为(
,当A的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ),L的最大值为
),L的最大值为![]() .
.
【解析】试题分析:(1)由题意知:抛物线过(0,0),所以将(0,0)代入y=x2+(2m﹣1)x+m2﹣1即可求得m的值,再由x<0时,y随x的增大而减小,可知对称轴一定在y轴的右侧,进而得出m的取值范围;
(2)①由AD∥x轴,所以A与D关于抛物线的对称轴对称,从而得出B的横坐标,代入抛物线解析式即可求得B的纵坐标,从而得出AB的长度;
②把A(a,b)代入y=x2﹣3x,所以b=a2﹣3a,利用对称性可求得D的坐标为(3﹣a,a2﹣3a),所以AD=|3﹣2a|,然后分以下两种情况讨论:0<a≤![]() 时和
时和![]() <a<3时,分别求出L与a的关系式后,利用二次函数的性质即可求出L的最值.
<a<3时,分别求出L与a的关系式后,利用二次函数的性质即可求出L的最值.
试题解析:解:(1)把(0,0)代入y=x2+(2m﹣1)x+m2﹣1,∴0=m2﹣1,∴m=±1,∵当x<0时,y随x的增大而减小,∴对称轴x=![]() >0,∴m<
>0,∴m<![]() ,∴m=﹣1,∴抛物线的解析式为y=x2﹣3x;
,∴m=﹣1,∴抛物线的解析式为y=x2﹣3x;
(2)①∵AD∥x轴,∴A与D关于抛物线的对称轴对称,∵抛物线的对称轴为x=![]() ,BC=1
,BC=1
∴点B的横坐标为1,∴把x=1代入y=x2﹣3x,∴y=﹣2,∴AB=2,∴矩形ABCD的周长为:2×2+2×1=6;
②把A(a,b)代入y=x2﹣3x,∴b=a2﹣3a,∴A(a,a2﹣3a),令y=0代入y=x2﹣3x,∴x=0或x=3,∴由题意知:0<a<3,∴AB=3a﹣a2,由①可知:A与D关于x=![]() 对称,∴D的坐标为(3﹣a,a2﹣3a),∴AD=|3﹣a﹣a|=|3﹣2a|,分两种情况讨论:
对称,∴D的坐标为(3﹣a,a2﹣3a),∴AD=|3﹣a﹣a|=|3﹣2a|,分两种情况讨论:
当0<a≤![]() 时,∴AD=3﹣2a,∴L=2(AB+AD)=﹣2a2+2a+6=﹣2(a﹣
时,∴AD=3﹣2a,∴L=2(AB+AD)=﹣2a2+2a+6=﹣2(a﹣![]() )2+
)2+![]() ,当a=
,当a=![]() 时,L的最大值为
时,L的最大值为![]() ,此时A的坐标为(
,此时A的坐标为(![]() ,﹣
,﹣![]() );
);
当![]() <a<3时,∴AD=2a﹣3,∴L=2(AB+AD)=
<a<3时,∴AD=2a﹣3,∴L=2(AB+AD)=![]() =﹣2(a﹣
=﹣2(a﹣![]() )2+
)2+![]() ,当a=
,当a=![]() 时,L的最大值为
时,L的最大值为![]() ,此时A的坐标为(
,此时A的坐标为(![]() ,﹣
,﹣![]() ).
).
综上所述:L=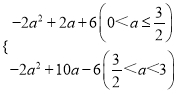 ,当A的坐标为(
,当A的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ),L的最大值为
),L的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高
 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心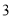 米.
米.
(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按
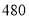 元销售时,每天可销售
元销售时,每天可销售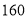 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出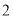 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为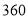 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润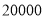 元?
元? -
科目: 来源: 题型:
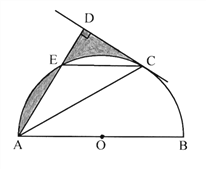
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD
 CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果正方形
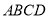 的边长为4,
的边长为4,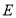 为
为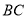 边上一点,
边上一点,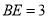 ,
,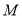 为线段
为线段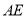 上一点,射线
上一点,射线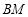 交正方形的一边于点
交正方形的一边于点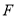 ,且
,且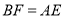 ,那么
,那么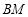 的长为__________.
的长为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠A
 ,P是BC边上的一点,
,P是BC边上的一点, ,
, 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结 ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E. ①若
 ,求
,求 的度数;
的度数; ②请直接写出∠A与
 的数量关系:___________________________;
的数量关系:___________________________; (2)如图2,在△ABC中,若∠BAC
 ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点 、
、 ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点 ,
, 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
相关试题

