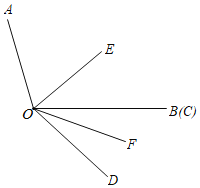
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
参考答案:
【答案】(1)∠EOF=75°;(2)∠AOE﹣∠BOF=35°;(3)∠AOE﹣∠BOF=35°.
【解析】
(1)直接利用角平分线的性质求出∠EOC和∠COF,相加即可求出答案;
(2)利用角平分线的性质求出∠AOE和∠COF,相减即可求出答案;
(3)当OC边绕O顺时针旋转时,∠AOB是变化的,∠AOB=110°+3°t,∠BOD是不变化的,所以∠AOE-∠BOF值是不变化的;
(1)∵OE平分∠AOC,OF平分∠BOD,
∴∠EOF=∠EOB+∠BOF=![]() ∠AOB+
∠AOB+![]() ∠BOD,
∠BOD,
∵∠AOB=110°,∠COD=40°,
∴∠EOF=75°;
(2)∵OE平分∠AOC,OF平分∠BOD,∠AOB=110°,∠COD=40°,
∴∠AOE=55°,∠BOF=20°,
∴∠AOE﹣∠BOF=35°;
(3)∵OF平分∠BOD,
∴∠BOF=![]() ∠BOD,
∠BOD,
∵∠AOB=110°,BO边绕点O以每秒3°的速度顺时针旋转t秒,
∴∠AOB=110°+3°t,∠BOF=![]() (40°+3°t),
(40°+3°t),
∴OE平分∠AOB,
∴∠AOE=![]() (110°+3°t),
(110°+3°t),
∴∠AOE﹣∠BOF=![]() (110°+3°t)﹣20°﹣
(110°+3°t)﹣20°﹣![]() t=35°,
t=35°,
∴在旋转过程中∠AOE﹣∠BOF的值是不会因t的变化而变化,∠AOE﹣∠BOF=35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.45元/分钟
0.4元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元.
(1)若小东乘坐滴滴快车,行车里程为20公里,行车时间为30分钟,则需付车费________元.
(2)若小明乘坐滴滴快车,行车里程为a公里,行车时间为b分钟,则小明应付车费多少元(用含a、b的代数式表示,并化简.)
(3)小王与小张各自乘坐滴滴快车,行车里程分别为9.5公里与14.5公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
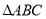 沿着过
沿着过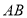 中点
中点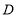 的直线折叠,使点
的直线折叠,使点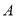 落在
落在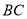 边上的
边上的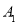 ,称为第
,称为第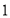 次操作,折痕
次操作,折痕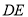 到
到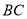 的距离记为
的距离记为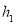 ;还原纸片后,再将
;还原纸片后,再将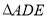 沿着过
沿着过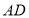 中点
中点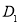 的直线折叠,使点
的直线折叠,使点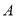 落在
落在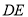 边上的
边上的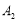 处,称为第
处,称为第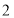 次操作,折痕
次操作,折痕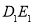 到
到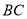 的距离记为
的距离记为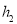 ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第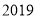 次操作后得到的折痕
次操作后得到的折痕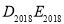 ,到
,到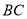 的距离记为
的距离记为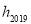 ,若
,若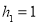 ,则
,则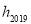 的值为( )
的值为( )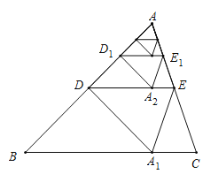
A.
 B.
B.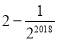 C.
C.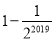 D.
D.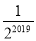
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(
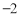 ,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
,0)、B两点,与y轴交于C点,其对称轴为直线x=1.(1)直接写出抛物线的解析式 :
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=
 .
.(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
 +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式. -
科目: 来源: 题型:
查看答案和解析>>【题目】用尺规在一个平行四边形内作菱形
 ,下列作法中错误的是( )
,下列作法中错误的是( )
A. (A) B. (B) C. (C) D. (D)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
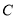 为线段
为线段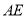 上一动点(不与点
上一动点(不与点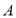 、
、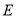 重合),在
重合),在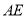 同侧分别作等边
同侧分别作等边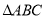 和等边
和等边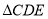 ,
,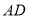 与
与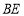 交于点
交于点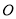 ,
,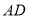 与
与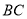 交于点
交于点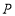 ,
,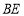 与
与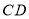 交于点
交于点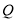 ,连接
,连接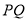 、
、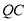 ,以下五个结论:①
,以下五个结论:① ;②
;②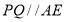 ;③
;③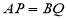 ;④
;④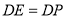 ;⑤
;⑤ 平分
平分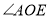 .一定成立的结论有______________;
.一定成立的结论有______________;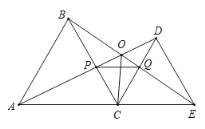
相关试题

