【题目】用尺规在一个平行四边形内作菱形![]() ,下列作法中错误的是( )
,下列作法中错误的是( )

A. (A) B. (B) C. (C) D. (D)
参考答案:
【答案】C
【解析】由作图,可以证明A、B、D中四边形ABCD是菱形,C中ABCD是平行四边形,即可得到结论.
A.∵AC是线段BD的垂直平分线,∴BO=OD,∴∠AOD=∠COB=90°.
∵AD∥BC,∴∠ADB=∠DBC,∴△AOD≌△COB,∴AO=OC,∴四边形ABCD是菱形.故A正确;
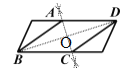
B.由作图可知:AD=AB=BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
∵AD=AB,∴四边形ABCD是菱形.故B正确;
C.由作图可知AB、CD是角平分线,可以得到ABCD是平行四边形,不能得到ABCD是菱形.故C错误;
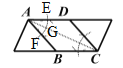
D.如图,∵AE=AF,AG=AG,EG=FG,∴△AEG≌△AFG,∴∠EAG=∠FAG.
∵AD∥BC,∴∠DAC=∠ACB,∴∠FAG=∠ACB,∴AB=BC,同理∠DCA=∠BCA,∴∠BAC=∠DCA,∴AB∥DC.
∵AD∥BC,∴四边形ABCD是平行四边形.
∵AB=BC,∴四边形ABCD是菱形.故D正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(
 ,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
,0)、B两点,与y轴交于C点,其对称轴为直线x=1.(1)直接写出抛物线的解析式 :
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
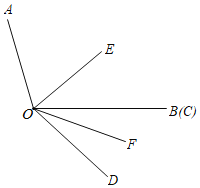
查看答案和解析>>【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=
 .
.(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
 +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
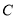 为线段
为线段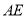 上一动点(不与点
上一动点(不与点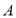 、
、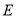 重合),在
重合),在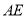 同侧分别作等边
同侧分别作等边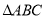 和等边
和等边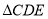 ,
,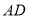 与
与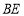 交于点
交于点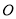 ,
,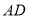 与
与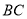 交于点
交于点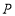 ,
,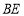 与
与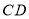 交于点
交于点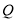 ,连接
,连接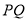 、
、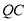 ,以下五个结论:①
,以下五个结论:① ;②
;②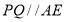 ;③
;③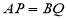 ;④
;④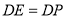 ;⑤
;⑤ 平分
平分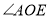 .一定成立的结论有______________;
.一定成立的结论有______________;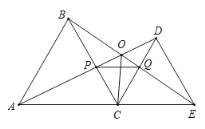
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是__________,据此判断该游戏__________(填“公平”或“不公平”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值
(单位:克)
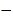 5
5 2
20
1
3
6
袋 数
1
4
3
4
5
3
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.
相关试题

