【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/公里 | 0.45元/分钟 | 0.4元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元. | |||
(1)若小东乘坐滴滴快车,行车里程为20公里,行车时间为30分钟,则需付车费________元.
(2)若小明乘坐滴滴快车,行车里程为a公里,行车时间为b分钟,则小明应付车费多少元(用含a、b的代数式表示,并化简.)
(3)小王与小张各自乘坐滴滴快车,行车里程分别为9.5公里与14.5公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差多少分钟?
参考答案:
【答案】(1)53.5;(2)![]() ,
,![]() ;
;![]() ,
,![]() ;(3)这两辆滴滴快车的行车时间相差24分钟.
;(3)这两辆滴滴快车的行车时间相差24分钟.
【解析】
(1)根据车费由里程费、时长费、远途费三部分组成进行计算即可.
(2)分![]() 和
和![]() 两种情况进行讨论即可.
两种情况进行讨论即可.
(3) 设小王行车时间为![]() 分,小张行车时间为
分,小张行车时间为![]() 分,根据他们的所付车费相同,列出方程,即可求解.
分,根据他们的所付车费相同,列出方程,即可求解.
(1)![]() (元),
(元),
故答案为:53.5
(2)当![]() 时,小明应付车费:
时,小明应付车费:![]() 元
元
当![]() 时,小明应付车费:
时,小明应付车费:
![]() 元
元
(3)设小王行车时间为![]() 分,小张行车时间为
分,小张行车时间为![]() 分,依题意有
分,依题意有
![]()
整理得![]()
![]()
答;这两辆滴滴快车的行车时间相差![]() 分.
分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
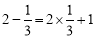 ,
,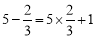 ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式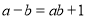 成立的一对有理数对“
成立的一对有理数对“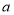 ,
,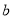 ”为“共生有理数对”,记为
”为“共生有理数对”,记为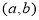 .
.(1)通过计算判断数对“-4,2”,“7,
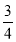 ”是不是“共生有理数对”;
”是不是“共生有理数对”;(2)若
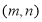 是“共生有理数对”,则“
是“共生有理数对”,则“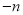 ,
,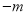 ”______(填“是”或“不是”)共生有理数对”,并说明理由.
”______(填“是”或“不是”)共生有理数对”,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
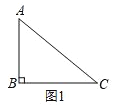
(1)如图1,在△ABC中,∠B=90,AB=3,BC=4,若△ABC的边上存在点P,使△ABP是以AB为腰的等腰三角形,则CP的长为______;
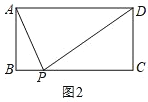
(2)如图2,在矩形ABCD中,AB=3,边BC上存在点P,使∠APD=90,求矩形ABCD面积的最小值.
问题解决:
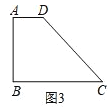
(3)如图3,在四边形ABCD中,AB=3,∠A=∠B=90,∠C=45,边CD上存在点P,使∠APB=60°,在此条件下,四边形ABCD的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
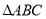 沿着过
沿着过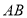 中点
中点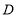 的直线折叠,使点
的直线折叠,使点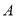 落在
落在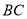 边上的
边上的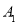 ,称为第
,称为第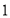 次操作,折痕
次操作,折痕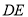 到
到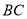 的距离记为
的距离记为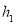 ;还原纸片后,再将
;还原纸片后,再将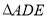 沿着过
沿着过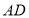 中点
中点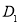 的直线折叠,使点
的直线折叠,使点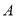 落在
落在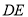 边上的
边上的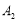 处,称为第
处,称为第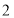 次操作,折痕
次操作,折痕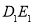 到
到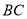 的距离记为
的距离记为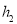 ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第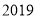 次操作后得到的折痕
次操作后得到的折痕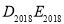 ,到
,到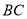 的距离记为
的距离记为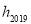 ,若
,若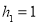 ,则
,则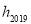 的值为( )
的值为( )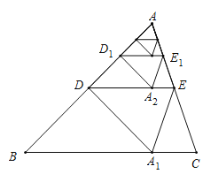
A.
 B.
B.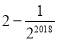 C.
C.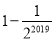 D.
D.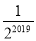
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(
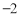 ,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
,0)、B两点,与y轴交于C点,其对称轴为直线x=1.(1)直接写出抛物线的解析式 :
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
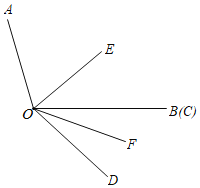
查看答案和解析>>【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
相关试题

