【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描点;
③连线.
(2)观察图象,当x 时,y随x的增大而增大;
(3)根据图象,不等式|x|<![]() x+
x+![]() 的解集为 .
的解集为 .
参考答案:
【答案】(1)见解析;(2)>0;(3)﹣1<x<3.
【解析】
(1)根据函数值填表即可;
(2)根据图象得出函数性质即可;
(3)根据图象得出不等式的解集即可.
(1)①填表正确
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 2 | 1 | 0 | 1 | 2 | 3 | … |
②③画函数图象如图所示:
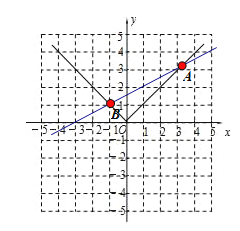
(2)由图象可得:x>0时,y随x的增大而增大;
(3)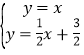 解得:
解得:![]() 所以A(3,3)
所以A(3,3)
同理B(-1,1)
由图象可得:不等式|x|<![]() 的解集为﹣1<x<3;
的解集为﹣1<x<3;
故答案为:>0;﹣1<x<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生对安全知识的掌握情况,学校随机抽取了20名学生进行安全知识测试,测试成绩(百分制)如下:
78、86、93、81、97、88、79、93、87、90、93、98、88、81、94、95、81、98、99、94
(1)根据上述数据,将下列表格补充完整(每组含最小值):
成绩/分
70~80
80~90
90~100
人数
7
(2)若用(1)中数据制作扇形统计图,求出表示“70~80”扇形的圆心角度数;
(3)已知该校共有2000名学生,若规定成绩90分及以上为优秀,估计该校学生对安全知识掌握情况为优秀的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示-5,点B表示10.动点P从点A出发,沿数轴正方向以每秒1个单位的速度匀速运动;同时,动点Q从点B出发,沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.
(1)当t为 秒时,P,Q两点相遇,求出相遇点所对应的数;
(2)当t为何值时,P,Q两点的距离为3个单位长度,并求出此时点P对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某一景点等候检票的时间,随机调查了部分游客,统计了他们进入该景点等候检票的时间,并绘制成如图表.
等候时间x(min)
频数(人数)
频率
10≤x<20
8
0.2
20≤x<30
14
a
30≤x<40
10
0.25
40≤x<50
b
0.125
50≤x<60
3
0.075
合计
40
1
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)根据上述图表制作扇形统计图,则“40≤x<50”所在扇形的圆心角度数是 °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为( )
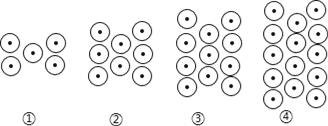
A. 2998 B. 3001 C. 3002 D. 3005
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:AB=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
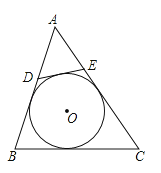
A.7
B.8
C.9
D.16
相关试题

