【题目】先阅读下列解题过程,然后解答问题(1)、(2)
解方程:|x+3|=2.
当x+30时,原方程可化为:x+3=2,解得x=1;
当x+3<0时,原方程可化为:x+3=2,解得x=5.
所以原方程的解是x=1,x=5.
(1)解方程:|3x1|5=0;
(2)探究:当b为何值时,方程|x2|=b+1①无解;②只有一个解;③有两个解.
参考答案:
【答案】(1)x=2或x=![]() ;(2)当b+1<0,即b<1时,方程无解;当b+1=0,即b=1时,方程只有一个解;当b+1>0,即b>1时,方程有两个解.
;(2)当b+1<0,即b<1时,方程无解;当b+1=0,即b=1时,方程只有一个解;当b+1>0,即b>1时,方程有两个解.
【解析】
(1)先移项得到|3x1|=5,利用绝对值的意义得到3x1=5或3x1=5,然后分别解两个一次方程;
(2)利用绝对值的意义讨论:当b+1<0或b+1=0或b+1>0时确定方程的解的个数,
(1)|3x1|=5,3x1=5或3x1=5,所以x=2或x=![]() ;
;
(2)∵|x2|≥0,
∴当b+1<0,即b<1时,方程无解;
当b+1=0,即b=1时,方程只有一个解;
当b+1>0,即b>1时,方程有两个解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有
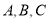 三点分别表示数
三点分别表示数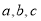 ,且
,且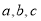 满足
满足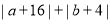
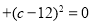 .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从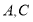 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为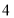 个单位/秒,乙的速度为
个单位/秒,乙的速度为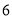 个单位/秒.
个单位/秒.(1)求
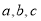 的值并在数轴上标出
的值并在数轴上标出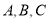 三点.
三点.
(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到
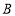 的距离为
的距离为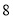 个单位?
个单位? -
科目: 来源: 题型:
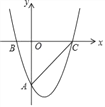
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,王先生家中买了一辆小轿车,他连接记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“-”,刚好50km的记为“0”.

(1)请求出这七天中平均每天行驶多少千米?
(2)若每行驶100km需用汽油6升,汽油价5.8元/升,请估计王先生家一个月(按30天计)的汽油费用是多少元?
-
科目: 来源: 题型:
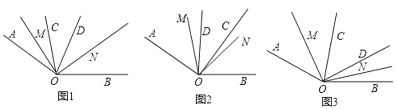
查看答案和解析>>【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=180°-α时,探索下面两个问题:
①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且CO在OD左侧时,直接写出∠MON的度数(用含α,k的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一动点的初始位置位于数轴上的原点,现对该动点做如下移动:第1次从原点向右移动1个单位长度至
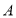 点,第2次从
点,第2次从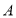 点向左移动3个单位长度至
点向左移动3个单位长度至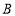 点,第3次从
点,第3次从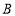 点向右移动6个单位长度至
点向右移动6个单位长度至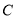 点,第4次从
点,第4次从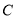 点向左移动9个单位长度至
点向左移动9个单位长度至 点,…依此类推,移动2020次后该动点在数轴上表示的的数为______.
点,…依此类推,移动2020次后该动点在数轴上表示的的数为______.
相关试题

