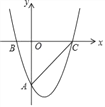
【题目】如图,抛物线y=![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣2x﹣6;(2)m=
x2﹣2x﹣6;(2)m=![]() ,M(3,﹣
,M(3,﹣![]() );(3)点P(2,﹣8),(﹣4,10),(1+
);(3)点P(2,﹣8),(﹣4,10),(1+![]() ,﹣5﹣
,﹣5﹣![]() ),(1﹣
),(1﹣![]() ,﹣5+
,﹣5+![]() ).
).
【解析】试题分析:(1)利用待定系数法求出二次函数的解析式;
(2)由直线向下平移m个单位得:y=x-6-m,由直线与抛物线有且只有一个公共点M可以知道:由解析式列方程组,根据△=0得出结论;
(3)分三种情况:
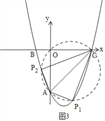
①当∠PAC=90°时,如图1,由△EAC是等腰直角三角形,可得E(-6,0),直线AP与抛物线的交点就是P,列方程组可得P点的坐标;
②当∠ACP=90°时,如图2,由PE=EC,列式:![]() x2-2x-6=-x-6,解出即可;
x2-2x-6=-x-6,解出即可;
③当∠APC=90°时,如图3,画图,根据直径所对的圆周角是直角,可知有两个点符合,设出P点的坐标,然后根据AC2,PA2,PC2的值,由勾股定理可得关于P点横、纵坐标的等量关系,联立抛物线的解析式,即可求出此时点P的坐标.
试题解析:解:(1)把点A(0,﹣6)、B(﹣2,0)代入抛物线y=![]() x2+bx+c中得:
x2+bx+c中得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣2x﹣6;
x2﹣2x﹣6;
(2)y=![]() x2﹣2x﹣6,
x2﹣2x﹣6,
当y=0时,![]() x2﹣2x﹣6=0,
x2﹣2x﹣6=0,
解得:x1=﹣2,x2=6,
∴C(6,0);
设直线AC的解析式为:y=kx+b,
则![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=x﹣6,
直线AC向下平移m个单位后的直线关系式为:y=x﹣6﹣m,
∵平移后的直线与抛物线有且只有一个公共点M,
则![]() ,
,
得:![]() =0,
=0,
△=(﹣3)2﹣4×![]() m=0,
m=0,
m=![]() ,
,
代入得:y=x﹣6﹣m=x﹣![]() ,
,
则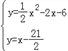 ,
,
解得:![]() ,
,
∴M(3,﹣![]() );
);
(3)分三种情况:
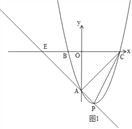
①当∠PAC=90°时,如图1,
∵OA=OC=6,∠AOC=90°,
∴△AOC是等腰直角三角形,
∴∠ACO=45°,
∴△EAC是等腰直角三角形,
∴AE=AC,
∴OE=OC=6,
∴E(﹣6,0),
设AE:y=kx+b,
则![]() ,解得:
,解得:![]() ,
,
∴直线AE的解析式为:y=﹣x﹣6,
则![]() ,
,
![]() ﹣2x﹣6=﹣x﹣6,
﹣2x﹣6=﹣x﹣6,
解得:x1=0(舍),x2=2,
∴P(2,﹣8),
②当∠ACP=90°时,如图2,
∠PCB=90°﹣45°=45°,
过P作PE⊥BC于E,
∴△PEC是等腰直角三角形,
∴PE=EC,
设P(x,![]() x2﹣2x﹣6),
x2﹣2x﹣6),
∴PE=![]() x2﹣2x﹣6,EC=﹣x﹣6,
x2﹣2x﹣6,EC=﹣x﹣6,
∴![]() x2﹣2x﹣6=﹣x﹣6,
x2﹣2x﹣6=﹣x﹣6,
解得:x1=6,x2=﹣4,
∵P在第二象限,
∴x=6不符合题意,舍去,x=﹣4,
∴P(﹣4,10),
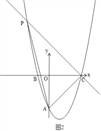
③以AC为直径画圆,交抛物线于两点P1、P2,如图3,
则∠AP1C=∠AP2C=90°,
∵![]() =
=![]() ,
,
![]() =
=![]() ,
,
AC2=62+62=72,
由勾股定理得:![]() +
+![]() =72,
=72,
化简得:x3﹣8x2+8x+24=0,
x3﹣2x2﹣4x﹣(6x2﹣12x﹣24)=0,
x(x2﹣2x﹣4)﹣6(x2﹣2x﹣4)=0,
(x﹣6)(x2﹣2x﹣4)=0,
解得:x1=6(舍),x2=1+![]() ,x3=1﹣
,x3=1﹣![]() ,
,
∴P(1+![]() ,﹣5﹣
,﹣5﹣![]() )或(1﹣
)或(1﹣![]() ,﹣5+
,﹣5+![]() ),
),
综上所述,△PAC为直角三角形时,点P的坐标为:(2,﹣8),(﹣4,10),(1+![]() ,﹣5﹣
,﹣5﹣![]() ),(1﹣
),(1﹣![]() ,﹣5+
,﹣5+![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点,且P关于原点的对称点P′恰好也落在该抛物线上,则点P′的坐标为( )
A. (﹣1,﹣1) B. (﹣2,﹣
 ) C. (﹣
) C. (﹣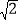 ,﹣2
,﹣2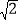 ﹣1) D. (﹣
﹣1) D. (﹣ ,﹣2
,﹣2 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方
形,然后按图②的方式拼成一个正方形。
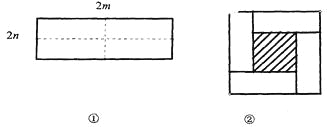
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出
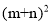 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有
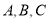 三点分别表示数
三点分别表示数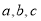 ,且
,且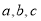 满足
满足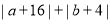
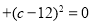 .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从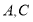 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为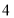 个单位/秒,乙的速度为
个单位/秒,乙的速度为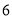 个单位/秒.
个单位/秒.(1)求
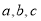 的值并在数轴上标出
的值并在数轴上标出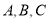 三点.
三点.
(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到
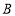 的距离为
的距离为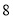 个单位?
个单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答问题(1)、(2)
解方程:|x+3|=2.
当x+30时,原方程可化为:x+3=2,解得x=1;
当x+3<0时,原方程可化为:x+3=2,解得x=5.
所以原方程的解是x=1,x=5.
(1)解方程:|3x1|5=0;
(2)探究:当b为何值时,方程|x2|=b+1①无解;②只有一个解;③有两个解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,王先生家中买了一辆小轿车,他连接记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“-”,刚好50km的记为“0”.

(1)请求出这七天中平均每天行驶多少千米?
(2)若每行驶100km需用汽油6升,汽油价5.8元/升,请估计王先生家一个月(按30天计)的汽油费用是多少元?
相关试题

