【题目】已知数轴上有![]() 三点分别表示数
三点分别表示数![]() ,且
,且![]() 满足
满足![]()
![]() .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从![]() 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为![]() 个单位/秒,乙的速度为
个单位/秒,乙的速度为![]() 个单位/秒.
个单位/秒.
(1)求![]() 的值并在数轴上标出
的值并在数轴上标出![]() 三点.
三点.

(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到![]() 的距离为
的距离为![]() 个单位?
个单位?
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)甲、乙在数轴上的点
;(2)甲、乙在数轴上的点![]() 相遇;(3)
相遇;(3)![]() 秒或
秒或![]() 秒后,甲到
秒后,甲到![]() 的距离为
的距离为![]() 个单位.
个单位.
【解析】
(1)根据![]()
![]() 中非负性分别求出a,b,c的值,并标出;
中非负性分别求出a,b,c的值,并标出;
(2)可设x秒后甲与乙相遇,根据甲与乙的路程和为28,可列出方程求解即可;
(3)分为两种情况:甲在B左侧8个单位和甲在B右侧8个单位讨论即可.
解:(1)∵![]()
![]() ,
,
∴a+16=0,b+4=0,c-12=0,
∴A:a=-16,B:b=-4,C:c=12,
在数轴上表示是:

(2)设甲、乙x秒后相遇,
∵数轴上AC相距(16+12)=28个单位,
∴可得:(4+6)x=28,
解得x=2.8,
∴-16+2.8×4=-4.8,
即甲、乙两点在-4.8处相遇;
(3)当甲在点B左侧8个单位时,
![]() (秒)
(秒)
当甲在点B右侧8个单位时,
![]() (秒)
(秒)
综上:![]() 秒或
秒或![]() 秒后,甲到
秒后,甲到![]() 的距离为
的距离为![]() 个单位.
个单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( )
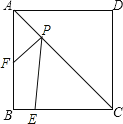
A. 2
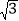 B. 4 C.
B. 4 C. 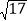 D. 2
D. 2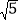
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点,且P关于原点的对称点P′恰好也落在该抛物线上,则点P′的坐标为( )
A. (﹣1,﹣1) B. (﹣2,﹣
 ) C. (﹣
) C. (﹣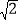 ,﹣2
,﹣2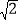 ﹣1) D. (﹣
﹣1) D. (﹣ ,﹣2
,﹣2 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方
形,然后按图②的方式拼成一个正方形。
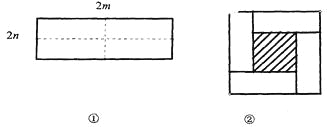
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出
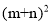 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答问题(1)、(2)
解方程:|x+3|=2.
当x+30时,原方程可化为:x+3=2,解得x=1;
当x+3<0时,原方程可化为:x+3=2,解得x=5.
所以原方程的解是x=1,x=5.
(1)解方程:|3x1|5=0;
(2)探究:当b为何值时,方程|x2|=b+1①无解;②只有一个解;③有两个解.
相关试题

