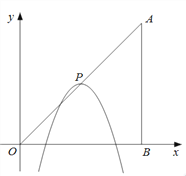
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线![]() 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动.
(1)当点P在线段OA上运动时,抛物线![]() 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).
①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线![]() 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.
参考答案:
【答案】(1)①![]() ;②-30≤c≤
;②-30≤c≤![]() ;(2)
;(2)![]() 或一般式(
或一般式(![]() ).
).
【解析】试题分析:(1)待定系数法求出OA直线,再求出二次函数顶点坐标的关系,求范围.(2) 当点P在线段OA上或者线段AB上时,分别讨论,求出二次函数表达式.
试题解析:
(1)①设直线OA所对应的函数表达为y=kx.
∵A(6,6)
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() .
.
∵y=-(x-m)2+n的顶点P在OA上,
∴![]() .
.
②由题意得:,y=-x2+2mx-m2+m.
∵抛物线与![]() 轴交点坐标为(0,
轴交点坐标为(0, ![]() ),
),
![]() .
.
∵点P在线段OA上,
∴0≤![]() ≤6.
≤6.
![]() ,
,
∵0<![]() <6,
<6,
∴当![]() .
.
当![]() .
.
∴c的取值范围为-30≤c≤![]() .
.
(2)当点P在线段OA上时,
∵抛物线经过B(6,0),
∴-(6-m)2+m=0,
∴.m1=4,m2=9,
∴ y=-(x-4)2+4或一般式(y=-x2+8x-12).
当点P在线段AB上时,
点P与点B重合,
∴m=6.
∴ y=-(x-6)2或一般式(y=-x2+12x-36).
-
科目: 来源: 题型:
查看答案和解析>>【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
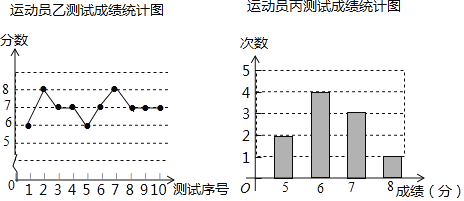
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为
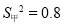 、
、 、
、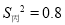 )
)(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=k1x+b与反比例函数y=
 的图象交于第一象限内的P(
的图象交于第一象限内的P( ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若
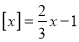 ,则x为_________.
,则x为_________.(4)已知x、y满足方程组
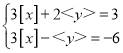
 ,求x、y的取值范围.
,求x、y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级学生参加了一次“运算能力”比赛,共有400名学生参加,参赛学生的成
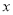 均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图:
均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图: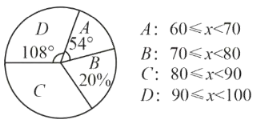
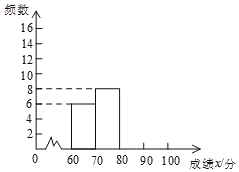
请根据所给信息,解答下列问题:
(1)所抽取分析的学生数量为 人;
(2)成绩为
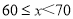 这一组的人数占体体人数的百分比为 ;
这一组的人数占体体人数的百分比为 ;(3)成绩为
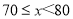 这一组的所在的扇形的圆心角度数为 ;
这一组的所在的扇形的圆心角度数为 ;(4)请补全频数分布直方图;
(5)若成绩达到90分或以上为“优秀”等级,则参加这次比赛的学生中属于“优秀”等级的约有 人 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用
 (元)与种植面积
(元)与种植面积 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.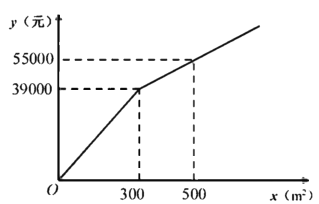
(1)直接写出当
 和
和 时,
时, 与
与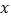 的函数关系式;
的函数关系式;(2)广场上甲、乙两种花卉的种植面积共
 ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在
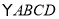 中,对角线
中,对角线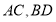 交于点
交于点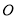 ,将过点
,将过点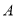 的直线
的直线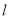 绕点
绕点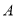 旋转,交射线
旋转,交射线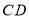 于点
于点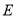 ,
,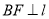 于点
于点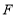 ,
,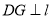 于点
于点 ,连接
,连接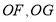 .
.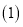 如图
如图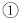 当点
当点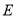 与点
与点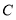 重合时,请直接写出线段
重合时,请直接写出线段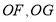 的数量关系;
的数量关系;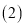 如图
如图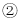 ,当点
,当点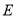 在线段
在线段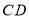 上时,
上时,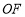 与
与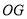 有什么数量关系?请说明你的结论;
有什么数量关系?请说明你的结论; 如图
如图 ,当点
,当点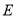 在线段
在线段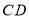 的延长线上时,
的延长线上时,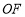 与
与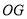 有什么数量关系?请说明你的结论.
有什么数量关系?请说明你的结论.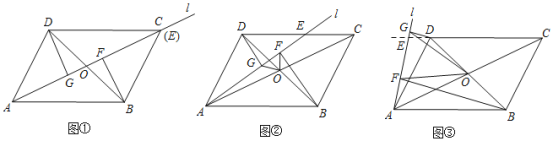
相关试题

