【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
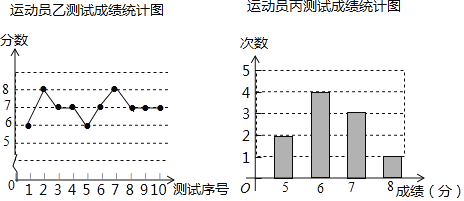
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
参考答案:
【答案】(1)7;7(2)选乙运动员更合适(3)![]()
【解析】
试题分析:(1)观察表格可知甲运动员测试成绩的众数和中位数都是(7分);
(2)易知![]() =7(分),
=7(分),![]() =7(分),
=7(分),![]() =6.3(分),根据题意不难判断;
=6.3(分),根据题意不难判断;
(3)画出树状图,即可解决问题;
试题解析:(1)甲运动员测试成绩的众数和中位数都是(7分).
(2)∵![]() =7(分),
=7(分),![]() =7(分),
=7(分),![]() =6.3(分),
=6.3(分),
∴![]() =
=![]() >
>![]() ,
,![]() >
>![]()
∴选乙运动员更合适.
(3)树状图如图所示,

第三轮结束时球回到甲手中的概率是P(求回到甲手中)=![]() .
.
-
科目: 来源: 题型:
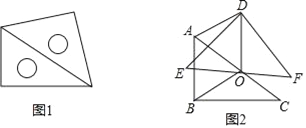
查看答案和解析>>【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:
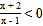 ;
;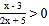 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:(1)若
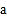 >0,
>0,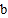 >0,则
>0,则 >0;若
>0;若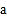 <0,
<0,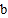 <0,则
<0,则 >0;
>0;(2)若
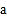 >0,
>0,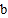 <0,则
<0,则 <0;若
<0;若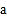 <0,
<0,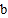 >0,则
>0,则 <0.
<0.反之:(1)若
 >0,则
>0,则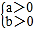 或
或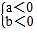
(2)若
 <0,则__________或__________.
<0,则__________或__________.(3)根据上述规律,求不等式
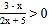 的解集.
的解集.(4)试求不等式
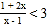 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
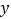 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=k1x+b与反比例函数y=
 的图象交于第一象限内的P(
的图象交于第一象限内的P( ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若
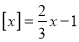 ,则x为_________.
,则x为_________.(4)已知x、y满足方程组
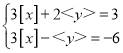
 ,求x、y的取值范围.
,求x、y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线
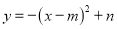 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动. (1)当点P在线段OA上运动时,抛物线
 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线
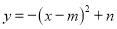 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.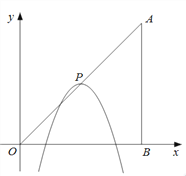
相关试题

