【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
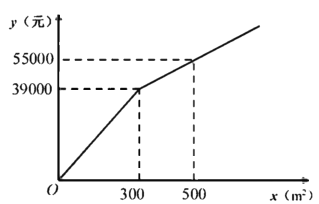
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
参考答案:
【答案】(1)![]() ;(2)应分配甲种花卉种植面积为
;(2)应分配甲种花卉种植面积为![]() ,乙种花卉种植面积为
,乙种花卉种植面积为![]() ,才能使种植总费用最少,最少总费用为119000元.
,才能使种植总费用最少,最少总费用为119000元.
【解析】(1)由图可知y与x的函数关系式是分段函数,待定系数法求解析式即可.
(2)设甲种花卉种植为 a m2,则乙种花卉种植(12000-a)m2,根据实际意义可以确定a的范围,结合种植费用y(元)与种植面积x(m2)之间的函数关系可以分类讨论最少费用为多少.
(1)![]()
(2)设甲种花卉种植面积为![]() ,则乙种花卉种植面积为
,则乙种花卉种植面积为![]() .
.
![]()
![]() .
.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 元.
元.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 元.
元.
![]() ,
,![]() 当
当![]() 时,总费用最低,最低为119000元.
时,总费用最低,最低为119000元.
此时乙种花卉种植面积为![]() .
.
答:应分配甲种花卉种植面积为![]() ,乙种花卉种植面积为
,乙种花卉种植面积为![]() ,才能使种植总费用最少,最少总费用为119000元.
,才能使种植总费用最少,最少总费用为119000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若
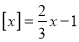 ,则x为_________.
,则x为_________.(4)已知x、y满足方程组
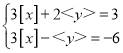
 ,求x、y的取值范围.
,求x、y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线
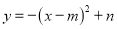 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动. (1)当点P在线段OA上运动时,抛物线
 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线
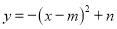 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.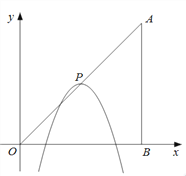
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级学生参加了一次“运算能力”比赛,共有400名学生参加,参赛学生的成
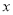 均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图:
均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图: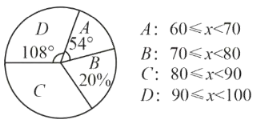
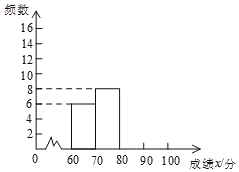
请根据所给信息,解答下列问题:
(1)所抽取分析的学生数量为 人;
(2)成绩为
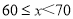 这一组的人数占体体人数的百分比为 ;
这一组的人数占体体人数的百分比为 ;(3)成绩为
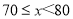 这一组的所在的扇形的圆心角度数为 ;
这一组的所在的扇形的圆心角度数为 ;(4)请补全频数分布直方图;
(5)若成绩达到90分或以上为“优秀”等级,则参加这次比赛的学生中属于“优秀”等级的约有 人 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
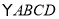 中,对角线
中,对角线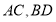 交于点
交于点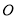 ,将过点
,将过点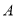 的直线
的直线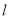 绕点
绕点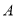 旋转,交射线
旋转,交射线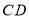 于点
于点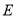 ,
,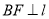 于点
于点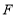 ,
,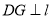 于点
于点 ,连接
,连接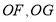 .
.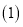 如图
如图 当点
当点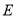 与点
与点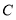 重合时,请直接写出线段
重合时,请直接写出线段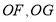 的数量关系;
的数量关系; 如图
如图 ,当点
,当点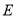 在线段
在线段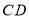 上时,
上时,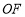 与
与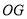 有什么数量关系?请说明你的结论;
有什么数量关系?请说明你的结论;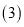 如图
如图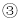 ,当点
,当点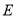 在线段
在线段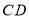 的延长线上时,
的延长线上时,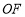 与
与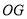 有什么数量关系?请说明你的结论.
有什么数量关系?请说明你的结论.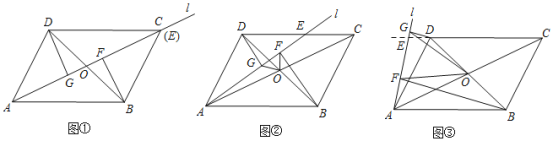
-
科目: 来源: 题型:
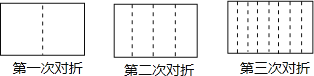
查看答案和解析>>【题目】将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,
(1)折一折,数一数,连续对折四次后,可以得到多少条折痕?
(2)想一想,如果对折n次,可以得到多少条折痕?
(3)如果能对折10次,可以得到多少条折痕?
(4)如果对折n次,可以得到多少个一样大小的小长方形?
-
科目: 来源: 题型:
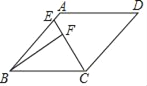
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=45°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为点F.
(1)当点F落在AB上时,求∠BCF的度数;
(2)若∠EBF=15°,求CF的长;
(3)当点E从点A运动到点B时,求点F运动的路径长.
相关试题

