【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

参考答案:
【答案】(1)y=﹣2x+9;(2)(-![]() ,﹣8);(3)
,﹣8);(3)![]()
【解析】试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,∴把点P(![]() ,8)代入
,8)代入![]() 可得:k2=4,∴反比例函数的表达式为
可得:k2=4,∴反比例函数的表达式为![]() ,∴Q (4,1).
,∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入
,8),Q (4,1)分别代入![]() 中,得:
中,得: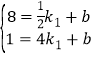 ,解得:
,解得:![]() ,∴一次函数的表达式为y=﹣2x+9;
,∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(![]() ,﹣8),∴OD=
,﹣8),∴OD=![]() ,P′D=8,∵点A在y=﹣2x+9的图象上,∴点A(
,P′D=8,∵点A在y=﹣2x+9的图象上,∴点A(![]() ,0),即OA=
,0),即OA=![]() ,∴DA=5,∴P′A=
,∴DA=5,∴P′A=![]() =
=![]() ,∴sin∠P′AD=
,∴sin∠P′AD=![]() =
=![]() ,∴sin∠P′AO=
,∴sin∠P′AO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:
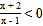 ;
;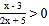 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:(1)若
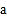 >0,
>0,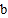 >0,则
>0,则 >0;若
>0;若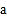 <0,
<0,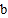 <0,则
<0,则 >0;
>0;(2)若
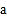 >0,
>0,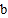 <0,则
<0,则 <0;若
<0;若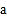 <0,
<0,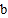 >0,则
>0,则 <0.
<0.反之:(1)若
 >0,则
>0,则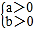 或
或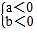
(2)若
 <0,则__________或__________.
<0,则__________或__________.(3)根据上述规律,求不等式
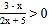 的解集.
的解集.(4)试求不等式
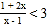 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
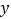 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

-
科目: 来源: 题型:
查看答案和解析>>【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
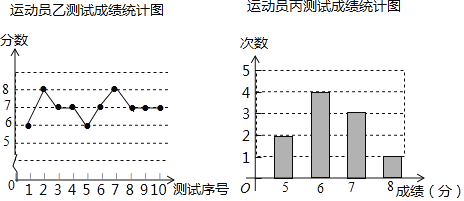
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为
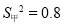 、
、 、
、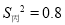 )
)(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若
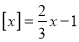 ,则x为_________.
,则x为_________.(4)已知x、y满足方程组
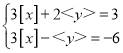
 ,求x、y的取值范围.
,求x、y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线
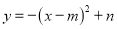 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动. (1)当点P在线段OA上运动时,抛物线
 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线
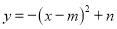 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.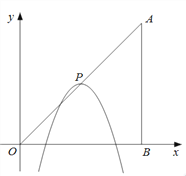
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级学生参加了一次“运算能力”比赛,共有400名学生参加,参赛学生的成
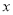 均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图:
均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图: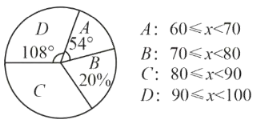
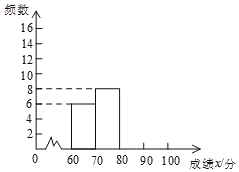
请根据所给信息,解答下列问题:
(1)所抽取分析的学生数量为 人;
(2)成绩为
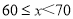 这一组的人数占体体人数的百分比为 ;
这一组的人数占体体人数的百分比为 ;(3)成绩为
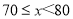 这一组的所在的扇形的圆心角度数为 ;
这一组的所在的扇形的圆心角度数为 ;(4)请补全频数分布直方图;
(5)若成绩达到90分或以上为“优秀”等级,则参加这次比赛的学生中属于“优秀”等级的约有 人 .
相关试题

