【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( ) 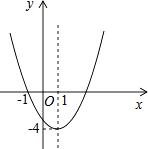
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
参考答案:
【答案】D
【解析】解:A、观察图象,可知抛物线的对称轴为直线x=1,则图象关于直线x=1对称,正确,故本选项不符合题意; B、观察图象,可知抛物线的顶点坐标为(1,﹣4),又抛物线开口向上,所以函数y=ax2+bx+c(a≠0)的最小值是﹣4,正确,故本选项不符合题意;
C、由图象可知抛物线与x轴的一个交点为(﹣1,0),而对称轴为直线x=1,所以抛物线与x轴的另外一个交点为(3,0),则﹣1和3是方程ax2+bx+c=0(a≠0)的两个根,正确,故本选项不符合题意;
D、由抛物线的对称轴为x=1,所以当x<1时,y随x的增大而减小,错误,故本选项符合题意.
故选D.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.
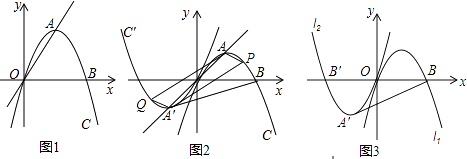
(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2 , l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学做一道数学题,已知两个多项式A、B,B=3x2y-5xy+x+7,试求A+B,这位同学把A+B看成A-B,结果求出的答案为6x2y+12xy-2x-9.
(1)请你替这位同学求出的正确答案;
(2)当x取任意数值,A-3B的值是一个定值,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费________元(用含a、n的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水40m3 ,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3 ,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:

(1)2018在第________行,第________列;
(2)由五个数组成的“
 ”中:
”中:① 这五个数的和可能是2019吗,为什么?
② 如果这五个数的和是60,直接写出这五个数;
(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
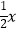 与双曲线y=
与双曲线y= 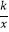 (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= 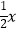 向上平移4个单位长度后,与y轴交于点C,与双曲线y=
向上平移4个单位长度后,与y轴交于点C,与双曲线y= 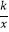 (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )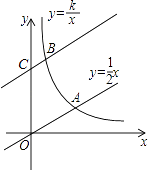
A.3
B.6
C.
D.
相关试题

