【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.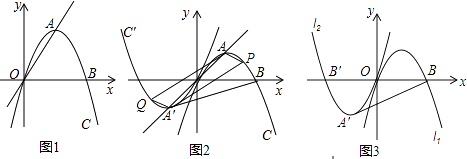
(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2 , l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:如图1,
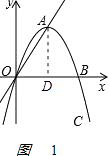
过A作AD⊥OB于D点,
∵抛物线l1:y=ax2+bx+c(a<0)过原点和B(4,0).
顶点为A.OD= ![]() OB=2.
OB=2.
又∵直线OA的解析式为y=x,
∴AD=OD=2.
∴点A的坐标为(2,2),
将A、B、O的坐标代入y=ax2+bx+c(a<0)中,
![]() ,
,
解得 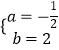 ,
,
∴抛物线C的解析式为y=﹣ ![]() x2+2x
x2+2x
(2)
解:如图2,
 ,
,
∵AO=A′O,PO=OQ,
∴四边形PAQA′是平行四边形,
∴S平行四边形PAQA′=4S△AOP.
过点P作PE⊥y轴于E交AO于F.
设P(x,﹣ ![]() x2+2x),则F(﹣
x2+2x),则F(﹣ ![]() x2+2x,﹣
x2+2x,﹣ ![]() x2+2x),
x2+2x),
若P点在抛物线AB段(2<x≤4)时,S△AOP= ![]() |xP﹣xF|×|yA|=
|xP﹣xF|×|yA|= ![]() [x﹣(﹣
[x﹣(﹣ ![]() x2+2x)]×2=
x2+2x)]×2= ![]() x2﹣x,
x2﹣x,
则S平行四边形PAQA′=4S△AOP=2x2﹣4x(2<x≤4)
(3)
解:如图3,
 ,
,
作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),由旋转的性质,得l2的顶点坐标A′(﹣2,﹣2),
故A′B的中点M的坐标(1,﹣1).
作MT⊥x轴于T,在Rt△NMB中,MT⊥NB于T,
∠NMT+∠BMT=90°,∠TBM+∠BMT=90°,
∴∠NMT=∠TBM,
又∵∠NTM=∠BTM=90°,
∴△MTN∽△BTM,
![]() =
= ![]() ,
,
MT2=TNTB,即12=(1﹣n)(4﹣1).
∴n= ![]() ,即N点的坐标为(
,即N点的坐标为( ![]() ,0).
,0).
直线l过点M(1,﹣1)、N( ![]() ,0),
,0),
∴直线l的解析式为y=﹣3x﹣2.
解 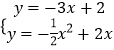 ,得x=5
,得x=5 ![]() .
.
在抛物线l1上存在两点使得HB=HA′,其坐标分别为(5+ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ),(5﹣
),(5﹣ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ).
).
解 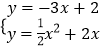 得x=﹣5
得x=﹣5 ![]() ,在抛物线l2上存在两点使得HB=HA′,其坐标分别为(﹣5+
,在抛物线l2上存在两点使得HB=HA′,其坐标分别为(﹣5+ ![]() ,17﹣3
,17﹣3 ![]() ),(﹣5﹣
),(﹣5﹣ ![]() ,17+3
,17+3 ![]() );
);
综上所述:(5+ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ),(5﹣
),(5﹣ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ),(﹣5+
),(﹣5+ ![]() ,17﹣3
,17﹣3 ![]() ),(﹣5﹣
),(﹣5﹣ ![]() ,17+3
,17+3 ![]() )
)
【解析】(1)根据O、B关于对称轴对称,可得OD的长,根据A在直线y=x上,可得A点坐标,根据待定系数法,可得答案;(2)根据平行四边形的性质,可得S平行四边形PAQA′=4S△AOP , 根据平行于x轴的直线上两点间的距离是较大的横坐标减较小的横坐标,可得PF的长,根据三角形的面积,可得答案;(3)根据线段垂直平分线上的点到线段两端点的距离相等,可得H在线段A′B的垂直平分线上,根据解方程组,可得H点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系xoy中,直线l与x、y轴分别交于点A(4,0)、B(0,
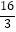 )两点,∠BAO的角平分线交y轴于点D.点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
)两点,∠BAO的角平分线交y轴于点D.点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E. 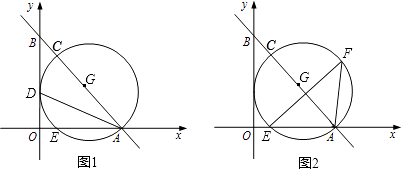
(1)求证:y轴是⊙G的切线;
(2)请求⊙G的半径r,并直接写出点C的坐标;
(3)如图2,若点F为⊙G上的一点,连接AF,且满足∠FEA=45°,请求出EF的长? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果直角三角形一条直角边长为23,斜边和另一条直角边长的长度都是整数,则这个直角三角形斜边的长为_________________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.
(1)试判断△ABC的形状.
(2)求AB边上的高。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学做一道数学题,已知两个多项式A、B,B=3x2y-5xy+x+7,试求A+B,这位同学把A+B看成A-B,结果求出的答案为6x2y+12xy-2x-9.
(1)请你替这位同学求出的正确答案;
(2)当x取任意数值,A-3B的值是一个定值,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费________元(用含a、n的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水40m3 ,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3 ,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
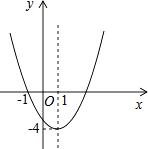
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
相关试题

