【题目】某同学做一道数学题,已知两个多项式A、B,B=3x2y-5xy+x+7,试求A+B,这位同学把A+B看成A-B,结果求出的答案为6x2y+12xy-2x-9.
(1)请你替这位同学求出的正确答案;
(2)当x取任意数值,A-3B的值是一个定值,求y的值.
参考答案:
【答案】(1) 12 x2y+2xy+5;(2)![]() .
.
【解析】
(1)由于A-B=6x2y+12xy-2x-9,所以A=B+6x2y+12xy-2x-9,因为B=3x2y-5xy+x+7,所以可以求得A,然后计算A+B即可.
(2)先根据(1)中A的值,求出A-3B,将含x的项合并,并使x的系数等于0,即可求出y.
解:(1)由题意可知:A=6x2y+12xy-2x-9+(3x2y-5xy+x+7)
=6x2y+12xy-2x-9+3x2y-5xy+x+7
=9x2y+7xy-x-2.
∴A+B=9x2y+7xy-x-2+(3x2y-5xy+x+7)
=9x2y+7xy-x-2+3x2y-5xy+x+7
=12 x2y+2xy+5.
(2)A-3B=9x2y+7xy-x-2-3(3x2y-5xy+x+7)
=9x2y+7xy-x-2-9x2y+15xy-3x-21
=22xy-4x-23
=(22y-4)x-23.
∵当x取任意数值,A-3B的值是一个定值,
∴22y-4=0.
解得:![]() .
.
故答案为:(1) 12 x2y+2xy+5;(2)![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国邮政部门规定:国内平信
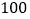 克以内(包括
克以内(包括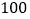 克)每
克)每 克需贴邮票
克需贴邮票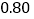 元,不足
元,不足 克重的以
克重的以 克计算;超过
克计算;超过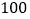 克的,超过部分每
克的,超过部分每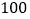 克需加贴
克需加贴 元,不足
元,不足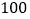 克的以
克的以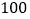 克计算.
克计算. 寄一封重
寄一封重 克的国内平信,需贴邮票多少元?
克的国内平信,需贴邮票多少元?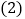 某人寄一封国内平信贴了
某人寄一封国内平信贴了 元邮票,此信重约多少克?
元邮票,此信重约多少克? 有
有 人参加一次数学竞赛,每份答卷重
人参加一次数学竞赛,每份答卷重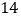 克,每个信封重
克,每个信封重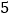 克,将这
克,将这 份答卷分装两个信封寄出,怎样装才能使所贴邮票金额最少?
份答卷分装两个信封寄出,怎样装才能使所贴邮票金额最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家
 月份用水量和交费情况:
月份用水量和交费情况:月份





用水量(吨)




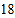
费用(元)





根据表格中提供的信息,回答以下问题:
 求出规定吨数和两种收费标准;
求出规定吨数和两种收费标准; 若小明家
若小明家 月份用水
月份用水 吨,则应缴多少元?
吨,则应缴多少元? 若小明家
若小明家 月份缴水费
月份缴水费 元,则
元,则 月份用水多少吨?
月份用水多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(1)求这个二次函数的解析式;
(2)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(3)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量
单价
不超过12 m3的部分
a元∕m3
超过12 m3但不超过20 m3的部分
1.5a元∕m3
超过20 m3的部分
2a元∕m3
(1) 当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2) 设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费_____________元(用含a、n的整式表示);
(3) 当a=2时,甲、乙两用户一个月共用水40 m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
相关试题

