搜索
【题目】用适当的方法计算：
（1）0.36＋(－7.4)＋0.5＋(－0.6)＋0.14；
（2）(－2.125)＋
＋(－3.2)；
（3）
.
（4）|－0.75|＋(－3)－(－0.25)＋
.
（5）
参考答案：
【答案】（1）-7；（2）3；（3）
；（4）-1；（5）
【解析】
利用有理数混合运算法则以及简便算法解答即可，利用加法交换律解（1）（2）（3）（4）更简便.
(1)0.36＋(－7.4)＋0.5＋(－0.6)＋0.14；
解：原式＝(0.36＋0.14)＋[(－7.4)＋(－0.6)]＋0.5
＝0.5＋(－8)＋0.5
＝－7.
(2)(－2.125)＋(＋3
)＋(＋5
)＋(－3.2)；
解：原式＝[(－2.125)＋(＋5)]＋[(＋3)＋(－3.2)]
＝3.
(3)(－2
)＋(＋3
)＋(－3
)＋(＋2
)＋(－1
)＋(＋1
).
解：原式＝[(－2)＋(－3)]＋[(＋3)＋(＋2)]＋[(－1)＋(＋1)]
＝(－6)＋6＋(－
)
＝－.
（4）|－0.75|＋(－3)－(－0.25)＋|－|＋
.
解：原式＝0.75－3＋0.25＋＋
＝(0.75＋0.25)＋(＋)－3
＝1＋1－3
＝－1.
(5)(－81)÷(＋3)×(－
)÷(－1
)；
解：原式＝－81÷
×÷
＝－81×
××
＝－10
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有依次排列的3个数：6，2，8，先将任意相邻的两个数，都用右边减去左边的数，所得之差写在这两个数之间，可产生一个新的数串：6，-4，2，6，8这称为第一次操作；做第二次同样操作后也可产生一个新数串：6，-10，-4，6，2，4，6，2，8，继续依次操作下去，问：从数串中6，2，8开始操作第2019次后所产生的那个新数串的所有数之和是( )
A.4054B.4056C.4058D.4060
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形
中，
，
，
且以
为边向外作正方形，其面积分别为
，若
，
，则
的值为（ ）
A. 24B. 36C. 48D. 60
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图甲，有两个形状完全相同的直角三角形ABC和EFG叠放在一起（点A与点E重合），已知AC
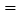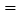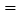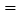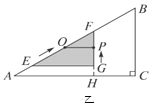
8 cm，BC6 cm，∠C90°，EG4 cm，∠EGF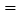90°，O是△EFG斜边上的中点. 如图乙，若整个△EFG从图甲的位置出发，以1 cm/s的速度沿射线AB方向平移，在△EFG平移的同时，点P从△EFG的顶点G出发，以1 cm/s的速度在直角边GF上向点F运动，当点P到达点F时，点P停止运动，△EFG也随之停止平移. 设运动时间为x（s），FG的延长线交AC于H，四边形OAHP的面积为y（cm2）（提示：不考虑点P与G、F重合的情况）.（1）当x为何值时，OP∥AC?
（2）求y与x之间的函数关系式，并确定自变量x的取值范围；
（3）是否存在某一时刻，使四边形OAHP面积与△ABC面积的比为
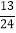？若存在，求出x的值；若不存在，说明理由.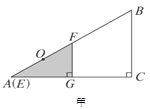
-
科目： 来源： 题型：
查看答案和解析>>【题目】正方形ABCD中，点M是直线BC上的一个动点（不与点B，C重合），作射线DM，过点B作BN⊥DM于点N，连接CN．
（1）如图1，当点M在BC上时，如果∠CDM=25°，那么∠MBN的度数是 ．
（2）如图2，当点M在BC的延长线上时，
①依题意补全图2；
②用等式表示线段NB，NC和ND之间的数量关系，并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（ ）
A. 4个 B. 3个 C. 2个 D. 1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】某客运站行车时刻表如图，若全程保持匀速行驶，则当快车出发______小时后，两车相距25km.
哈尔滨—长春
出发时间
到站时间
里程（km）
普通车
7:00
11:00
300
快车
7:30
10:30
300
相关试题
