【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 且以
且以![]() 为边向外作正方形,其面积分别为
为边向外作正方形,其面积分别为![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )

A. 24B. 36C. 48D. 60
参考答案:
【答案】C
【解析】
过D点作DE∥AB,由平行四边形的判定和性质可得△DEC是直接三角形,然后根据勾股定理可得三边关系,从而可求三个正方形的面积的关系,继而求得答案.
解:
![]()
过D点作DE∥AB,
∴四边形ABED是平行四边形,
∴AD=BE,AB=DE,∠B=∠DEC,
∵∠ABC+∠DCB=90°,
∴∠DEC+∠DCE=90°,
∴∠EDC=90°,
∵BC=2AD,
∴AD=EC,
在RT△DEC中,
∵EC2=DE2+DC2,
∴(![]() )2=AB2+DC2,
)2=AB2+DC2,
∴![]() =S1 +S3,
=S1 +S3,
∵S1=3,S3=9,
∴S2=48.
故本题答案应为:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:对于排好顺序的三个数:
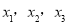 称为数列
称为数列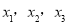 .将这个数列如下式进行计算:
.将这个数列如下式进行计算: 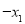 ,
,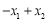 ,
,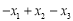 ,所得的三个新数中,最大的那个数称为数列
,所得的三个新数中,最大的那个数称为数列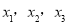 的“关联数值”.
的“关联数值”.例如:对于数列
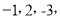 因为
因为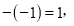
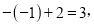
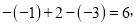 所以数列
所以数列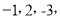 的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列
的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列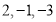 的 “关联数值”为0;数列
的 “关联数值”为0;数列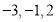 的“关联数值”为3...而对于“
的“关联数值”为3...而对于“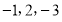 ”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.(1)数列
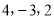 的“关联数值”为_______;
的“关联数值”为_______; (2)将“
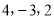 ”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______(3)将“
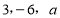 ”
”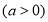 这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求
这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求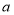 的值,并写出取得“关联数值”最大值的数列.
的值,并写出取得“关联数值”最大值的数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 为正方形
为正方形 的边
的边 上一点,将正方形
上一点,将正方形 沿
沿 折叠,点
折叠,点 落在点
落在点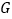 处,连接并延长
处,连接并延长 ,交
,交 于点
于点 ,求证:
,求证: ;
;(2)如图2,点
 分别在
分别在 边上,且
边上,且 ,求证:
,求证:
(3)如图3,点
 分别在
分别在 边上,点
边上,点 分别在
分别在 边上,
边上, 交
交 于点
于点 ,已知
,已知 ,
, ,
,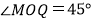 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有依次排列的3个数:6,2,8,先将任意相邻的两个数,都用右边减去左边的数,所得之差写在这两个数之间,可产生一个新的数串:6,-4,2,6,8这称为第一次操作;做第二次同样操作后也可产生一个新数串:6,-10,-4,6,2,4,6,2,8,继续依次操作下去,问:从数串中6,2,8开始操作第2019次后所产生的那个新数串的所有数之和是( )
A.4054B.4056C.4058D.4060
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC
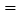 8 cm,BC
8 cm,BC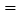 6 cm,∠C
6 cm,∠C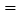 90°,EG
90°,EG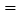 4 cm,∠EGF
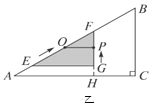
4 cm,∠EGF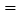 90°,O是△EFG斜边上的中点. 如图乙,若整个△EFG从图甲的位置出发,以1 cm/s的速度沿射线AB方向平移,在△EFG平移的同时,点P从△EFG的顶点G出发,以1 cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移. 设运动时间为x(s),FG的延长线交AC于H,四边形OAHP的面积为y(cm2)(提示:不考虑点P与G、F重合的情况).
90°,O是△EFG斜边上的中点. 如图乙,若整个△EFG从图甲的位置出发,以1 cm/s的速度沿射线AB方向平移,在△EFG平移的同时,点P从△EFG的顶点G出发,以1 cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移. 设运动时间为x(s),FG的延长线交AC于H,四边形OAHP的面积为y(cm2)(提示:不考虑点P与G、F重合的情况).(1)当x为何值时,OP∥AC?
(2)求y与x之间的函数关系式,并确定自变量x的取值范围;
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为
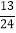 ?若存在,求出x的值;若不存在,说明理由.
?若存在,求出x的值;若不存在,说明理由.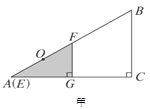
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法计算:
(1)0.36+(-7.4)+0.5+(-0.6)+0.14;
(2)(-2.125)+
 +(-3.2);
+(-3.2);(3)
 .
.(4)|-0.75|+(-3)-(-0.25)+
 .
.(5)

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点M是直线BC上的一个动点(不与点B,C重合),作射线DM,过点B作BN⊥DM于点N,连接CN.
(1)如图1,当点M在BC上时,如果∠CDM=25°,那么∠MBN的度数是 .
(2)如图2,当点M在BC的延长线上时,
①依题意补全图2;
②用等式表示线段NB,NC和ND之间的数量关系,并证明.

相关试题

