【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
参考答案:
【答案】(1)、SSS;(2)、证明过程见解析;(3)、答案见解析
【解析】
试题分析:(1)、本题都是作线段相等,则根据SSS来判定三角形全等;(2)、根据垂直得出∠OMP=∠ONP=90°,然后结合OP=OP,OM=ON得出直角三角形全等;(3)、根据三角形全等的性质得出角平分线.
试题解析:(1)、SSS
(2)、小聪的作法正确
∵PM⊥OM , PN⊥ON ∴∠OMP=∠ONP=90°在Rt△OMP和Rt△ONP中 ∵OP=OP ,OM=ON
∴Rt△OMP≌Rt△ONP(HL) ∴∠MOP=∠NOP ∴OP平分∠AOB
(3)、如图所示.
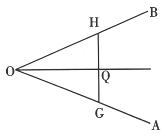
步骤:①利用刻度尺在OA、OB上分别截取OG=OH. ②连结GH,利用刻度尺找出GH的中点Q.
③作射线OQ.则OQ为∠AOB的平分线.
-
科目: 来源: 题型:
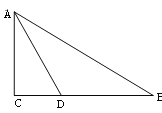
查看答案和解析>>【题目】如图,在
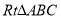 中,
中,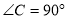 ,
,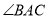 的角平分线
的角平分线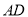 交
交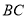 于
于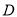 .
.
(1)动手操作:利用尺规作⊙O,使⊙O经过点
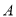 、
、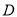 ,且圆心
,且圆心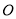 在
在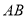 上;并标出⊙O与
上;并标出⊙O与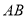 的另一个交点
的另一个交点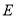 (保留作图痕迹, 不写作法);
(保留作图痕迹, 不写作法);(2)综合应用:在你所作的图中,①判断直线BC与⊙O的位置关系,并说明理由;② 若
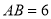 ,
,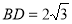 ,求线段
,求线段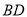 、
、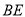 与劣弧所围成的图形面积(结果保留根号和
与劣弧所围成的图形面积(结果保留根号和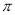 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
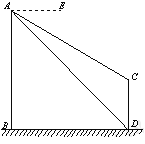
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数
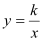 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)直线AO的解析式;
(2)求反比例函数解析式;
⑶求点C的坐标.
-
科目: 来源: 题型:
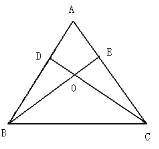
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
A.当a<1时,点B在⊙A外
B.当1<a<5时,点B在⊙A内
C.当a<5时,点B在⊙A内
D.当a>5时,点B在⊙A外 -
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是( )
A.5 B.6 C.7 D.8
相关试题

