【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
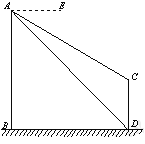
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
参考答案:
【答案】(1)60米;(2)![]() 米.
米.
【解析】
试题分析:(1)根据平行线的性质可以得到:∠BAD=∠ADB=45°,根据等腰直角三角形的性质可以求出BD的长度;
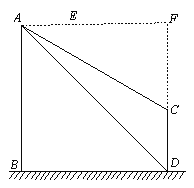
(2)延长AE、DC交于点F,可知四边形ABDF是正方形,根据tan∠CAF=![]() ,求出CF的长度,再根据DF的长度求出CD的高度.
,求出CF的长度,再根据DF的长度求出CD的高度.
试题解析:(1)根据题意得BD∥AE,
∴∠ADB=∠EAD=45°.
∵∠ABD=90°,
∴∠BAD=∠ADB=45°.
∴BD=AD=60(米).
∴两建筑物两底部之间的水平距离BD的长度为60米
(2)延长AE、DC交于点F,
根据题意可知四边形ABDF是正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
由tan∠CAF=![]() ,
,
得CF=AFtan∠CAF
=60tan30°
=60×![]() =20
=20![]() .
.
又∵DF=60,
∴CD=60-20![]() .
.
∴建筑物CD的高度为(60-20![]() )米.
)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(二)班5位女生的体重(单位:kg)分别是:36,37,39,41,41.则这组数据的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 是正方形,
是正方形, 与
与 相交于点
相交于点 ,点
,点 、
、 是直线
是直线 上两动点,且
上两动点,且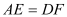 ,
, 所在直线与对角线
所在直线与对角线 所在直线交于点
所在直线交于点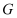 ,连接
,连接 ,直线
,直线 交
交 于点
于点 .
.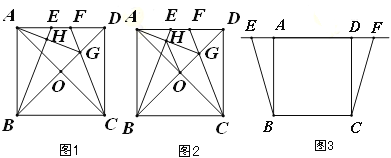
(1)如图1,当点
 、
、 在线段
在线段 上时,
上时,①求证:
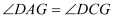 ;
;②猜想
 与
与 的位置关系,并加以证明;
的位置关系,并加以证明;(2)如图2,在(1)条件下,连接
 ,试说明
,试说明 平分
平分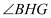 ;
;(3)当点
 、
、 运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出
运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
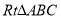 中,
中,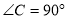 ,
,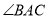 的角平分线
的角平分线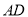 交
交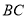 于
于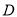 .
.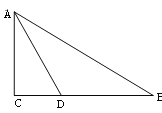
(1)动手操作:利用尺规作⊙O,使⊙O经过点
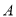 、
、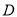 ,且圆心
,且圆心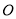 在
在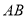 上;并标出⊙O与
上;并标出⊙O与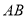 的另一个交点
的另一个交点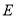 (保留作图痕迹, 不写作法);
(保留作图痕迹, 不写作法);(2)综合应用:在你所作的图中,①判断直线BC与⊙O的位置关系,并说明理由;② 若
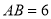 ,
,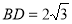 ,求线段
,求线段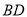 、
、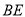 与劣弧所围成的图形面积(结果保留根号和
与劣弧所围成的图形面积(结果保留根号和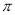 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数
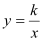 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)直线AO的解析式;
(2)求反比例函数解析式;
⑶求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
-
科目: 来源: 题型:
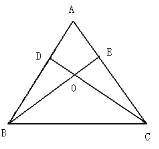
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
相关试题

