【题目】如图,在![]() 中,
中,![]() ,
,![]() 的角平分线
的角平分线![]() 交
交![]() 于
于![]() .
.
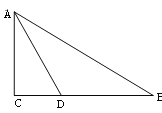
(1)动手操作:利用尺规作⊙O,使⊙O经过点![]() 、
、![]() ,且圆心
,且圆心![]() 在
在![]() 上;并标出⊙O与
上;并标出⊙O与![]() 的另一个交点
的另一个交点![]() (保留作图痕迹, 不写作法);
(保留作图痕迹, 不写作法);
(2)综合应用:在你所作的图中,①判断直线BC与⊙O的位置关系,并说明理由;② 若![]() ,
,![]() ,求线段
,求线段![]() 、
、![]() 与劣弧所围成的图形面积(结果保留根号和
与劣弧所围成的图形面积(结果保留根号和![]() ).
).
参考答案:
【答案】(1)作图见解析;(2)①证明见解析;②![]() .
.
【解析】
试题分析:(1)作AD的垂直平分线交AB于点O,以点O为圆心,OA为半径画圆;
(2)根据角平分线的性质可以证明∠DAC=∠ODA,从而可证OD∥AC,从而可证OD⊥BC,所以可证BC与⊙O相切;用△ODB的面积减去扇形ODE的面积得到阴影的面积.
试题解析:(1)如图,作⊙O 标出点E
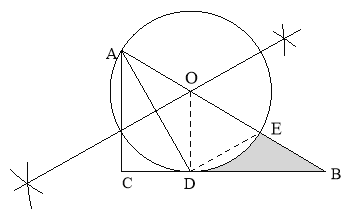
(2)①BC与⊙O相切.
理由如下:连结OD.
∵AD平分∠BAC
∴∠DAC=∠DAB
∵OA=OD
∴∠ODA=∠DAB
∴∠DAC=∠ODA
∴OD∥AC
∴∠ODB=∠C
∵∠C=90
∴∠ODB=90
∴OD⊥BC
∴ BC与⊙O相切,
② 连结DE
设⊙O的半径为r,则OB=6-r,
在Rt△ODB中,∠ODB=90,
∴ 0B2=OD2+BD2
即:(6-r)2= r2+ (![]() )2
)2
∴r=2
在![]() 中,
中,![]()
∴∠DOB=60
∵△ODB的面积![]()
![]()
扇形ODE的面积![]()
![]()
∴线段![]() 、
、![]() 与劣弧所围成的图形面积为:
与劣弧所围成的图形面积为:
![]()
![]() -
-![]()
-
科目: 来源: 题型:
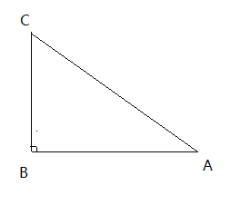
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm。
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.①当t=1秒时,求PQ的长;②从出发几秒钟后,△PQB是等腰三角形?
(2)若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(二)班5位女生的体重(单位:kg)分别是:36,37,39,41,41.则这组数据的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 是正方形,
是正方形, 与
与 相交于点
相交于点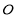 ,点
,点 、
、 是直线
是直线 上两动点,且
上两动点,且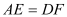 ,
, 所在直线与对角线
所在直线与对角线 所在直线交于点
所在直线交于点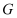 ,连接
,连接 ,直线
,直线 交
交 于点
于点 .
.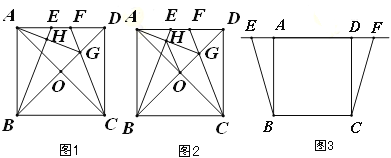
(1)如图1,当点
 、
、 在线段
在线段 上时,
上时,①求证:
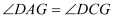 ;
;②猜想
 与
与 的位置关系,并加以证明;
的位置关系,并加以证明;(2)如图2,在(1)条件下,连接
 ,试说明
,试说明 平分
平分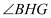 ;
;(3)当点
 、
、 运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出
运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
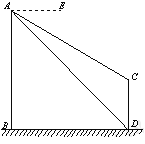
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数
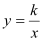 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)直线AO的解析式;
(2)求反比例函数解析式;
⑶求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
相关试题

