【题目】如图①,已知线段AB=20cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点

(1)若点C恰好是AB中点,则DE的长是多少?(直接写出结果)
(2)若BC=14cm,求DE的长
(3)试说明不论BC取何值(不超过20cm),DE的长不变
(4)知识迁移:如图②,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试求出∠DOE的大小,并说明∠DOE的大小与射线OC的位置是否有关?
参考答案:
【答案】(1)DE=10cm;(2)DE=10cm;(3)证明见详解;(4)∠DOE=65°,∠DOE的度数与射线OC的位置无关.
【解析】
(1)根据中点的性质求出AC、BC的长,根据线段中点的定义计算即可;
(2)根据中点的性质求出AC、BC的长,根据线段中点的定义计算即可;
(3)根据中点的性质求出AC、BC的长,根据线段中点的定义计算,即可说明DE的长不变;
(4)根据角平分线的定义得到∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() BOC,结合图形计算即可求出∠DOE的大小.
BOC,结合图形计算即可求出∠DOE的大小.
解:(1)∵点C恰为AB的中点,
∴AC=BC=![]() AB=10cm,
AB=10cm,
∵点D、E分别是AC和BC的中点,
∴DC=![]() AC=5cm,CE=
AC=5cm,CE=![]() BC=5cm,
BC=5cm,
∴DE=10cm.
(2)∵AB=20cm,BC=14cm,
∴AC=6cm,
∵点D、E分别是AC和BC的中点,
∴CD=3cm,CE=7cm,
∴DE=CD+CE=10cm;
(3)∵点D、E分别是AC和BC的中点,
∴CD=![]() AC,CE=
AC,CE=![]() BC,
BC,
∴DE=CD+CE=![]() (AC+BC)=
(AC+BC)=![]() AB=10cm,
AB=10cm,
∴不论AC取何值(不超过20cm),DE的长不变.
(4)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠COB,
∠COB,
∴∠DOE=∠DOC+∠COE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB,
∠AOB,
∵∠AOB=130°,
∴∠DOE=65°.
∴∠DOE的度数与射线OC的位置无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,A(1,0)、B(0,2),BA=BC,∠ABC=90°,则点 C 的坐标为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在
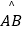 的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
的中点,连接AF并延长与CB的延长线相交于点G,连接OF. 
(1)求证:OF= BG;
BG;
(2)若AB=4,求DC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】与题干中平面图形有相同对称性的平面图形是( ).

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM=
 AB.
AB.
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 、
、  ,连接
,连接  、
、  ,若
,若 

 ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
相关试题

