【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装360辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练和2名新工人每月可安装12辆电动汽车;2名熟练工和3名新工人每月可安装21辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
参考答案:
【答案】(1)![]() (2)工厂有四种新工人的招聘方案,分别是招聘:2名新工人,4名新工人,6名新工人,8名新工人.(3)工厂应招聘4名新工人,工厂每月支出的工资总额W最小
(2)工厂有四种新工人的招聘方案,分别是招聘:2名新工人,4名新工人,6名新工人,8名新工人.(3)工厂应招聘4名新工人,工厂每月支出的工资总额W最小
【解析】
(1)设每名熟练工每月安装x辆电动汽车,每名新工人每月安装y辆电动汽车,根据条件建立二元一次方程组求出其解即可;
(2)设抽调m名熟练工与n名新聘工人刚好完成一年的安装任务,根据工人1年完成的总任务为360辆建立方程求出其解即可;
(3)根据工资总额=熟练工的工资×人数+新员工的工资×人数,可得出W关于n的函数关系式,再利用一次函数的性质即可解决最值问题.
解:(1)设每名熟练工每月安装x辆电动汽车,每名新工人每月安装y辆电动汽车.由题意得,![]()
解得:![]() .
.
答:每名熟练工每月安装6辆电动汽车,每名新工人每月安装3辆电动汽车;
(2)设抽调m名熟练工与n名新聘工人刚好完成一年的安装任务,
由题意得12(6m+3n)=360,
∴m=5-![]() .
.
∵m为正整数,
∴n为偶数.
∵0<n<10,
∴n=2,4,6,8,
∴m=4,3,2,1,
∴工厂有四种新工人的招聘方案,分别是招聘:2名新工人,4名新工人,6名新工人,8名新工人.
(3)根据题意得:W=1200n+(5-![]() n)×2000=200n+10000.
n)×2000=200n+10000.
∵要使新工人数量多于熟练工,
∴n=4、6、8.
∵200>0,w随n的增大而增大
∴当n=4时,W取最小值,
∴工厂应招聘4名新工人,工厂每月支出的工资总额W最小
-
科目: 来源: 题型:
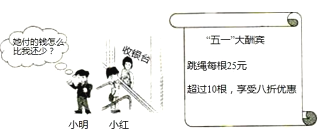
查看答案和解析>>【题目】试根据图中信息,解答下列问题:
(1)购买8根跳绳需________元,购买14根跳绳需________元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求小红购买跳绳的根数;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y=
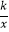 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+  .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠ ,求OP2的最小值.
,求OP2的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把一批货物用一列火车运往某地
 已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.
已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元. 设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围;
设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围; 已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离s(km)与慢车行驶时间t(h)之间的函数图象如图所示,则下列说法中:①甲、乙两地之间的距离为560km;②快车速度是慢车速度的1.5倍;③快车到达甲地时,慢车距离甲地60km;④相遇时,快车距甲地320km;正确的是( )
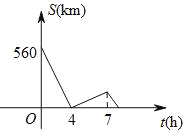
A. ①② B. ①③ C. ①④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=﹣
 x2﹣
x2﹣  x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
(1)求这条抛物线的解析式;
(2)如图2,D点在x轴上,且在A点的右侧,E点为抛物线上第二象限内的点,连接ED交抛物线于第二象限内的另外一点F,点E到y轴的距离与点F到y轴的距离之比为3:1,已知tan∠BDE= ,求点E的坐标;
,求点E的坐标;
(3)如图3,在(2)的条件下,点G由B出发,沿x轴负方向运动,连接EG,点H在线段EG上,连接DH,∠EDH=∠EGB,过点E作EK⊥DH,与抛物线相应点E,若EK=EG,求点K的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共50台,其中A型电脑的进货量不少于14台,B型电的进货量不少于A型电脑的2倍,那么该商店有几种进货方案?该商场购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m (0<m<100)元,若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这50台电脑销售总利润最大的进货方案.
相关试题

