【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离s(km)与慢车行驶时间t(h)之间的函数图象如图所示,则下列说法中:①甲、乙两地之间的距离为560km;②快车速度是慢车速度的1.5倍;③快车到达甲地时,慢车距离甲地60km;④相遇时,快车距甲地320km;正确的是( )
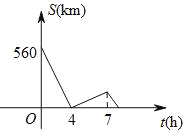
A. ①② B. ①③ C. ①④ D. ①③④
参考答案:
【答案】B
【解析】
根据函数图象直接得出甲乙两地之间的距离;根据题意得出慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;设慢车速度为3xkm/h,快车速度为4xkm/h,由(3x+4x)×4=560,可得x=20,从而得出快车的速度是80km/h,慢车的速度是60km/h.由题意可得出:快车和慢车相遇地离甲地的距离,当慢车行驶了7小时后,快车已到达甲地,可求出此时两车之间的距离即可.
由题意可得出:甲乙两地之间的距离为560千米,故①正确;
由题意可得出:慢车和快车经过4个小时后相遇,出发后两车之间的距离开始增大直到快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,故②错误;
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,x=20
∴快车的速度是80km/h,慢车的速度是60km/h.
由题意可得出:快车和慢车相遇地离甲地的距离为4×60=240km,故④错误,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240-3×60=60km,故③正确.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数,且皆有31项.若a2+b30=29,a30+b2=﹣9,则此两等差级数的和相加的结果为多少?( )
A.300
B.310
C.600
D.620 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示,直线l过点M(3,0)且平行于y轴.
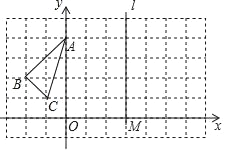
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求P1P2的长.(用含a的代数式表示)
(3)通过计算加以判断,PP2的长会不会随点P位置的变化而变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,BC=DC,∠A=90°,∠ABC=105°.若AB=5
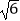 ,则△ABD外心与△BCD外心的距离为何?( )
,则△ABD外心与△BCD外心的距离为何?( ) 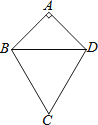
A.5
B.5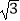
C.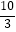
D.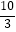
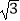

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )

A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,
 ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.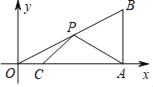
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元。
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售。设购买个x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由。
相关试题

