【题目】学校开展综合实践活动中,某班进行了小制作评比,作品上交时间为5月11日至5月30日,评委们把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图如下,小长方形的高之比为:2:5:2:1.现已知第二组的上交作品件数是20件.求:

(1)此班这次上交作品共 件;
(2)评委们一致认为第四组的作品质量都比较高,现从中随机抽取2件作品参加学校评比,小明的两件作品都在第四组中,他的两件作品都被抽中的概率是多少?(请写出解答过程)
参考答案:
【答案】(1)40(2)![]()
【解析】解:(1)40。
(2)第四组的作品的件数为![]() (件)。
(件)。
设四件作品编号为1、2、3、4号,小明的两件作品分别为1、2号。从中随机抽取2件作品的所有结果为(1,2);(1,3);(1,4); (2,3);(2,4);(3,4),小明的两件作品都被抽中的情况有1种,
∴他的两件作品都被抽中的概率是![]() 。
。
(1)用第二小组的频数除以该小组的份数占总份数的多少即可求得总人数:![]() 。
。
(2)根据频数、频率和总量的关系求出第四组的作品的件数,分别列举出所有可能结果后用概率的公式即可求解。
-
科目: 来源: 题型:
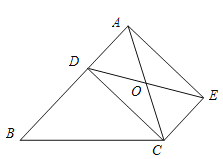
查看答案和解析>>【题目】如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
“
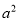 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如: 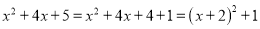 ,
,∵
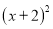 ≥0,
≥0,∴
 ≥1,
≥1,∴
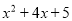 ≥1.
≥1.试利用“配方法”解决下列问题:
(1)填空:
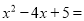 (x )2+ ;
(x )2+ ;(2) 已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
(3)比较代数式
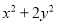 与
与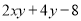 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为3和5,则这个三角形的周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形内接于
 ,点P在弧BC上,PA与BC相交于点D,若PB=3,PC=6,则PD=( )
,点P在弧BC上,PA与BC相交于点D,若PB=3,PC=6,则PD=( )
A. 1.5 B.
 C. 2 D.
C. 2 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
相关试题

