【题目】阅读下列材料:
“![]() ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如: ![]() ,
,
∵![]() ≥0,
≥0,
∴![]() ≥1,
≥1,
∴![]() ≥1.
≥1.
试利用“配方法”解决下列问题:
(1)填空: ![]() (x )2+ ;
(x )2+ ;
(2) 已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
(3)比较代数式![]() 与
与![]() 的大小.
的大小.
参考答案:
【答案】(1)-2,1,(2)5≤c<9(3)作差法,大于
【解析】分析:(1)利用完全平方公式变形即可
(2)由a2+b2=10a+8b﹣41,得(a﹣5)2+(b﹣4)2=0,结合非负数的性质求得a,b的值,然后利用三角形的三边关系求得c的取值范围即可;
(3)先作差,再配方,利用非负数的性质即可得出差>0,即可得到结论.
详解:(1)∵x2﹣4x+5= x2﹣4x+4+1=(x﹣2)2+1.故答案为:-2,1.
(2)∵a2+b2=10a+8b﹣41,∴a2﹣10a+25+b2﹣8b+16=0,即(a﹣5)2+(b﹣4)2=0,a﹣5=0,b﹣4=0,解得a=5,b=4.∵c是△ABC中最长的边,∴5≤c<9.
(3)![]() =
=![]()
=![]()
=![]()
∵![]() ≥0,
≥0, ![]() ≥0,∴
≥0,∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有质地均匀的A、B、C、D四张卡片,上面对应的图形分别是圆、正方形、正三角形、平行四边形,将这四张卡片放入不透明的盒子中摇匀,从中随机抽出一张(不放回),再随机抽出第二张.
(1)如果要求抽出的两张卡片上的图形,既有圆又有三角形,请你用列表或画树状图的方法,求出出现这种情况的概率;
(2)因为四张卡片上有两张上的图形,既是中心对称图形,又是轴对称图形,所以小明和小东约定做一个游戏,规则是:如果抽出的两个图形,既是中心对称图形又是轴对称图形,则小明赢;否则,小东赢.问这个游戏公平吗?为什么?如果不公平,请你设计一个公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
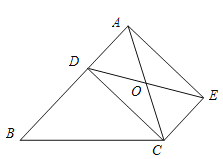
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为3和5,则这个三角形的周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校开展综合实践活动中,某班进行了小制作评比,作品上交时间为5月11日至5月30日,评委们把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图如下,小长方形的高之比为:2:5:2:1.现已知第二组的上交作品件数是20件.求:

(1)此班这次上交作品共 件;
(2)评委们一致认为第四组的作品质量都比较高,现从中随机抽取2件作品参加学校评比,小明的两件作品都在第四组中,他的两件作品都被抽中的概率是多少?(请写出解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形内接于
 ,点P在弧BC上,PA与BC相交于点D,若PB=3,PC=6,则PD=( )
,点P在弧BC上,PA与BC相交于点D,若PB=3,PC=6,则PD=( )
A. 1.5 B.
 C. 2 D.
C. 2 D. 
相关试题

