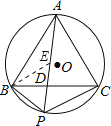
【题目】如图,等边三角形内接于![]() ,点P在弧BC上,PA与BC相交于点D,若PB=3,PC=6,则PD=( )
,点P在弧BC上,PA与BC相交于点D,若PB=3,PC=6,则PD=( )

A. 1.5 B. ![]() C. 2 D.
C. 2 D. ![]()
参考答案:
【答案】C
【解析】在PA上截取PE=PB,连接BE,
∵△ABC是等边三角形,∠ACB=APB,
∴∠APB=∠ACB=∠ABC=60°,AB=BC,
∴△BEP是等边三角形,BE=PE=PB,
∴∠ABC-∠EBC=∠EBP-∠EBC=60°-∠EBC;
∴∠ABE=∠CBP;
∵在△ABE与CBP中, 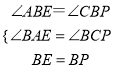 ,
,
∴△ABE≌△CBP,
∴AE=CP,
∴AP=AE+PE=PB+PC,
∵PB=3,PC=6,
∴PA=6+3=9,
∵∠BAP=∠DAB(公共角),
∠ABC=∠ACB=∠APB=60°,
∴△ABD∽△APB,
∴![]() ,
,
∴![]() ,
,
∴BD=![]() AB=
AB=![]() AC,
AC,
∵∠PBD=∠PAC,
∠BPD=∠APC=60°,
∴△BPD∽△APC,
∴![]() ,
,
∴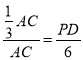 ,
,
∴PD=2,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
“
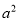 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如: 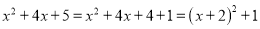 ,
,∵
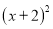 ≥0,
≥0,∴
 ≥1,
≥1,∴
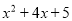 ≥1.
≥1.试利用“配方法”解决下列问题:
(1)填空:
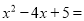 (x )2+ ;
(x )2+ ;(2) 已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
(3)比较代数式
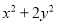 与
与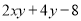 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为3和5,则这个三角形的周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校开展综合实践活动中,某班进行了小制作评比,作品上交时间为5月11日至5月30日,评委们把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图如下,小长方形的高之比为:2:5:2:1.现已知第二组的上交作品件数是20件.求:

(1)此班这次上交作品共 件;
(2)评委们一致认为第四组的作品质量都比较高,现从中随机抽取2件作品参加学校评比,小明的两件作品都在第四组中,他的两件作品都被抽中的概率是多少?(请写出解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货11吨;用1辆A型车和2辆B型车载满货物一次可运货13吨.根据以上信息, 解答下列问题:
(1)1辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车
 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都载满货物请用含有
辆,一次运完,且恰好每辆车都载满货物请用含有 的式子表示
的式子表示 ,并帮该物流公司设计租车方案;
,并帮该物流公司设计租车方案;(3)在(2)的条件下,若A型车每辆需租金500元/次,B型车每辆需租金600元/次.请选出最省钱的租车方案,并求出最少租车费用.
相关试题

