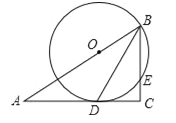
【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
参考答案:
【答案】(1)证明见解析;(2)12.
【解析】
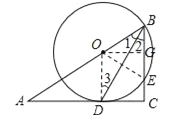
试题分析:(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直径,即可得证;
(2)过O作OG垂直于BE,可得出四边形ODCG为矩形,在直角三角形OBG中,利用勾股定理求出BG的长,由垂径定理可得BE=2BG.
试题解析:(1)证明:连接OD,∵BD为∠ABC平分线,∴∠1=∠2,∵OB=OD,∴∠1=∠3,∴∠2=∠3,∴OD∥BC,∵∠C=90°,∴∠ODA=90°,则AC为圆O的切线;
(2)过O作OG⊥BC,连接OE,∴四边形ODCG为矩形,∴GC=OD=OB=10,OG=CD=8,在Rt△OBG中,利用勾股定理得:BG=6,∵OG⊥BE,OB=OE,∴BE=2BG=12.
解得:BE=12.
-
科目: 来源: 题型:
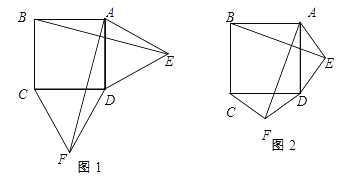
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC边
 上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°. 求∠ABC和∠BAC的度数.
上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°. 求∠ABC和∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然发生的事件是( )
A.明天会下雨
B.小明数学考试得99分
C.今天是星期一,明天就是星期二
D.明年有370天 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣4x+a=0有两个相同的实数根,则a的值是 .
-
科目: 来源: 题型:
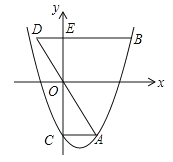
查看答案和解析>>【题目】如图,抛物线
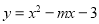 (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.(1)用含m的代数式表示BE的长.
(2)当m=
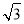 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
相关试题

