【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.

参考答案:
【答案】40°
【解析】试题分析:先根据∠A=50°,得到∠ABC+∠ACB=180°﹣50°=130°,再根据∠D=90°,可得∠DBC+∠DCB=90°,最后根据∠DBA+∠DCA=(∠ABC+∠ACB)﹣(∠DBC+∠DCB)进行计算即可.
试题解析:∵∠A=50°, ∴∠ABC+∠ACB=180°﹣50°=130°,
而∠D=90°,
∴∠DBC+∠DCB=90°,
∴∠DBA+∠DCA=(∠ABC+∠ACB)﹣(∠DBC+∠DCB)
=130°﹣90°
=40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC边
 上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°. 求∠ABC和∠BAC的度数.
上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°. 求∠ABC和∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然发生的事件是( )
A.明天会下雨
B.小明数学考试得99分
C.今天是星期一,明天就是星期二
D.明年有370天 -
科目: 来源: 题型:
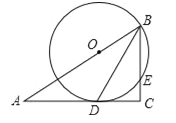
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣4x+a=0有两个相同的实数根,则a的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
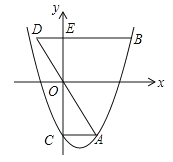
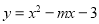 (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.(1)用含m的代数式表示BE的长.
(2)当m=
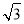 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2x2x7+3x5x4﹣xx8
(2)(m+3)(m﹣3)﹣(m+3)2
(3)(π﹣3)0﹣( )﹣1+(﹣5)3÷(﹣5)2
)﹣1+(﹣5)3÷(﹣5)2
(4)(1+2x﹣y)(2x+y﹣1)
相关试题

