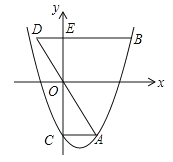
【题目】如图,抛物线![]() (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
参考答案:
【答案】(1)BE=2m;(2)点D在抛物线上;(3)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)根据A、C两点纵坐标相同,求出点A横坐标即可解决问题.
(2)求出点D坐标,然后判断即可.
(3)①首先根据EO=2FG,证明BG=2DE,列出方程即可解决问题.
②求出直线AE、BO的解析式,求出交点M的横坐标,列出方程即可解决问题.
试题解析:(1)∵C(0,﹣3),AC⊥OC,∴点A纵坐标为﹣3,y=﹣3时,![]() ,解得x=0或m,∴点A坐标(m,﹣3),∴AC=m,∴BE=2AC=2m.
,解得x=0或m,∴点A坐标(m,﹣3),∴AC=m,∴BE=2AC=2m.
(2)点D在抛物线上.理由如下:
∵m=![]() ,∴点A坐标(
,∴点A坐标(![]() ,﹣3),∴直线OA为
,﹣3),∴直线OA为![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∴点B坐标(
,∴点B坐标(![]() ,3),∴点D纵坐标为3,对于函数
,3),∴点D纵坐标为3,对于函数![]() ,当y=3时,x=
,当y=3时,x=![]() ,∴点D坐标(
,∴点D坐标(![]() ,3).∵对于函数
,3).∵对于函数![]() ,x=
,x=![]() 时,y=3,∴点D在抛物线上;
时,y=3,∴点D在抛物线上;
(3)①∵∠ACE=∠CEG=∠EGA=90°,∴四边形ECAG是矩形,∴EG=AC=BG,∵FG∥OE,∴OF=FB,∵EG=BG,∴EO=2FG,∵![]() DEEO=
DEEO=![]() GBGF,∴BG=2DE,∵DE∥AC,∴
GBGF,∴BG=2DE,∵DE∥AC,∴![]() =
=![]() ,∵点B坐标(2m,
,∵点B坐标(2m,![]() ),∴OC=2OE,∴3=2(
),∴OC=2OE,∴3=2(![]() ),∵m>0,∴m=
),∵m>0,∴m=![]() .
.
②∵A(m,﹣3),B(2m,![]() ),E(0,
),E(0,![]() ),∴直线AE解析式为
),∴直线AE解析式为![]() ,直线OB解析式为
,直线OB解析式为![]() ,由
,由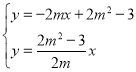 消去y得到
消去y得到![]() ,解得x=
,解得x=![]() ,∴点M横坐标为
,∴点M横坐标为![]() ,∵△AMF的面积=△BFG的面积,∴
,∵△AMF的面积=△BFG的面积,∴![]() ,整理得到:
,整理得到:![]() ,∵m>0,∴m=
,∵m>0,∴m=![]() .故答案为:
.故答案为:![]() .
.
-
科目: 来源: 题型:
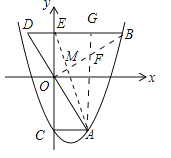
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣4x+a=0有两个相同的实数根,则a的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2x2x7+3x5x4﹣xx8
(2)(m+3)(m﹣3)﹣(m+3)2
(3)(π﹣3)0﹣( )﹣1+(﹣5)3÷(﹣5)2
)﹣1+(﹣5)3÷(﹣5)2
(4)(1+2x﹣y)(2x+y﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,从点D向AB、AC两边作垂线段,垂足分别为E、F,那么下列结论中错误的是 ( )
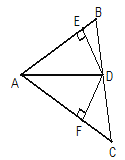
A. DE=DF B. AE=AF C. BD=CD D. ∠ADE=∠ADF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是圆O的弦,AB是直径,且CD⊥AB,垂足为P.
(1)求证:PC2=PAPB;
(2)PA=6,PC=3,求圆O的直径.

相关试题

