【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= . 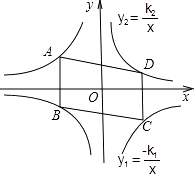
参考答案:
【答案】8
【解析】解:在ABCD中,AB∥CD,AB=CD(平行四边形的对应边平行且相等),故设A(x,y1)、B(x、y2),则根据反比例函数的图象关于原点对称的性质知,C(﹣x,﹣y1)、D(﹣x、﹣y2).
∵A在双曲线y1=﹣ ![]() 上,B在双曲线y2=
上,B在双曲线y2= ![]() 上,
上,
∴x=﹣ ![]() ,x=
,x= ![]() ,
,
∴﹣ ![]() =
= ![]() ;
;
又∵k1=2k2(k1>0),
∴y1=﹣2y2;
∵SABCD=24,
∴ ![]() |2x|=6|y2x|=24,
|2x|=6|y2x|=24,
解得,y2x=±4,
∵双曲线y2= ![]() 位于第一、三象限,
位于第一、三象限,
∴k2=4,
∴k1=2k2=8
故答案是:8.

【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下四个命题,其中原命题与逆命题均为真命题的个数是( )
①若
 ,
, ,则
,则 ;
; ②若
 ,则
,则 ;
;③角的平分线上的点到角的两边的距离相等;
④线段的垂直平分线上的点到线段两端点距离相等.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
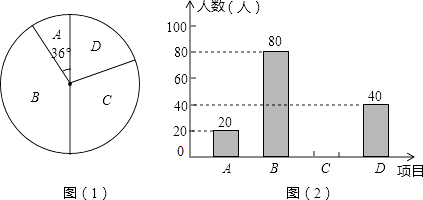
(1)这次被调查的学生共有人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴为直线x=1,给出下列结论: ①b2﹣4ac>0;②2a+b=0;③abc>0;④3a+c>0,
则正确的结论个数为( )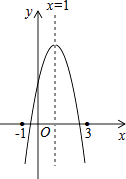
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
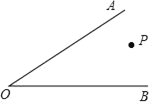
查看答案和解析>>【题目】∠AOB内部有一点P,∠AOB=60°.
(1)过点P画PC∥OB,交OA于点C;
(2)过点P画PD⊥OB,交OB于点D,交OA于点E;
(3)过点C画直线OB的垂线段CF;
(4)根据所画图形,∠ACF= 度,∠OED= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=﹣
 在第二象限内图象上一点,点B是反比例函数y=
在第二象限内图象上一点,点B是反比例函数y=  在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )

相关试题

