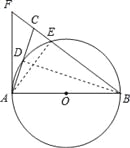
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

参考答案:
【答案】(1)证明见试题解析;(2)CE=2,AF=![]() .
.
【解析】试题分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2![]() )2=x2+(3x)2求得答案.
)2=x2+(3x)2求得答案.
试题解析:(1)证明:如图,连接BD.∵AB为⊙O的直径,∴∠ADB=90°,∴∠DAB+∠ABD=90°.∵AF是⊙O的切线,∴∠FAB=90°,即∠DAB+∠CAF=90°.∴∠CAF=∠ABD.∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.∴∠ABC=2∠CAF.
(2)如图,连接AE,∴∠AEB=90°,设CE=x,∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x,在Rt△ACE中,AC2=CE2+AE2,
即(2![]() )2=x2+(3x)2,∴x=2.∴CE=2.
)2=x2+(3x)2,∴x=2.∴CE=2.
-
科目: 来源: 题型:
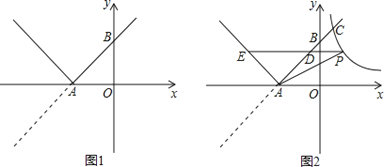
查看答案和解析>>【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于
 AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( ) 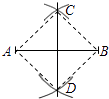
A.矩形
B.菱形
C.正方形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是线段
是线段 上一点,
上一点,  ,
,  .
.
(
 )
) __________
__________  ;
;(
 )动点
)动点 、
、 分别从
分别从 、
、 同时出发,点
同时出发,点 以
以 的速度沿
的速度沿 向右运动,终点为
向右运动,终点为 ;点
;点 以
以 的速度沿
的速度沿 向左运动,终点为
向左运动,终点为 .当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,
.当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,  、
、 、
、 三点,有一点恰好是以另两点为端点的线段的中点?
三点,有一点恰好是以另两点为端点的线段的中点? -
科目: 来源: 题型:
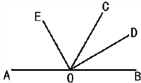
查看答案和解析>>【题目】如图,点O在直线AB上,OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____;∠BOD的余角是______;
(2)若∠AOC=118°,求∠COD的度数;
(3)射线OD与OE之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用网格画图:
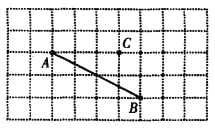
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系
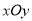 中,抛物线
中,抛物线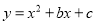 与
与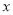 轴交于
轴交于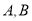 两点(点
两点(点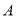 在点
在点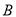 的左侧),与
的左侧),与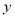 轴交于点
轴交于点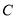 ,点
,点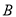 的坐标为
的坐标为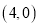 ,将直线
,将直线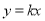 沿
沿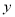 轴向上平移4个单位长度后恰好经过
轴向上平移4个单位长度后恰好经过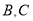 两点。
两点。(1)求直线
 及抛物线的解析式;
及抛物线的解析式;(2)将直线
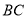 沿
沿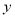 轴向上平移5个单位长度后与抛物线交于
轴向上平移5个单位长度后与抛物线交于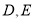 两点,若点
两点,若点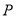 是抛物线位于直线
是抛物线位于直线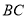 下方的一个动点,连接
下方的一个动点,连接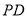 ,交直线
,交直线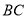 于点
于点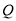 ,连接
,连接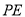 和
和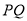 。设
。设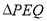 的面积为
的面积为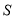 ,当S取得最大值时,求出此时点
,当S取得最大值时,求出此时点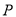 的坐标及
的坐标及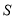 的最大值;
的最大值;(3)如图2,记(2)问中直线
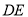 与
与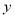 轴交于
轴交于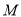 点,现有一点
点,现有一点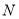 从
从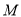 点出发,先沿
点出发,先沿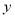 轴到达
轴到达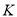 点,再沿
点,再沿 到达
到达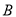 点,已知
点,已知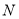 点在
点在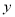 轴上运动的速度是每秒2个单位长度,它在直线
轴上运动的速度是每秒2个单位长度,它在直线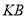 上运动速度是1个单位长度。现要使
上运动速度是1个单位长度。现要使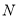 点按照上述要求到达
点按照上述要求到达 点所用的时间最短,请简述确定
点所用的时间最短,请简述确定 点位置的过程,求出点
点位置的过程,求出点 的坐标,不要求证明。
的坐标,不要求证明。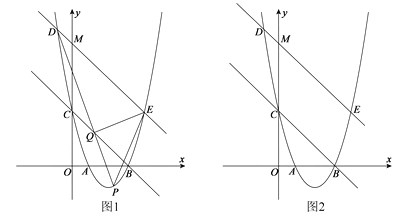
相关试题

