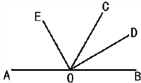
【题目】如图,点O在直线AB上,OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____;∠BOD的余角是______;
(2)若∠AOC=118°,求∠COD的度数;
(3)射线OD与OE之间有什么特殊的位置关系?为什么?
参考答案:
【答案】(1)BOE,∠AOE和∠COE;(2)31°;(3)OD⊥OE
【解析】试题分析:
(1)根据图形结合“补角的定义”可得∠AOE的补角是∠BOE;由OE、OD分别是∠AOC、∠BOC的平分线,可得∠COE=∠AOE=![]() ∠AOC,∠COD=∠BOD=
∠AOC,∠COD=∠BOD=![]() ∠BOC,从而可证得∠COE+∠COD=∠DOE=90°,由此可得∠BOD+∠COE=90°,∠BOD+∠AOE=90°,从而可知,∠BOD的余角是∠AOE和∠COE;
∠BOC,从而可证得∠COE+∠COD=∠DOE=90°,由此可得∠BOD+∠COE=90°,∠BOD+∠AOE=90°,从而可知,∠BOD的余角是∠AOE和∠COE;
(2)由∠AOC的度数可先求得∠BOC的度数,再由OD平分∠BOC即可得到∠COD的度数;
(3)由(1)可知∠DOE=90°,由此就可得到OE⊥OD.
试题解析:
(1)∵点O在直线AB上,
∴∠AOE+∠BOE=180°,∠AOC+∠BOC=180°,
∴∠AOE的补角是∠BOE.
∵OE、OD分别是∠AOC、∠BOC的平分线,
∴∠COE=∠AOE=![]() ∠AOC,∠COD=∠BOD=
∠AOC,∠COD=∠BOD=![]() ∠BOC,
∠BOC,
∴∠COE+∠COD=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=90°,
∠AOB=90°,
∴∠BOD+∠COE=90°,∠BOD+∠AOE=90°,
∴在图中,∠BOD的余角是∠AOE和∠COE;
(2)由(1)可知,∠AOC+∠BOC=180°,∠COD=∠BOD=![]() ∠BOC,
∠BOC,
∴∠BOC=180°-∠AOC=180°-118°=62°,
∴∠COD=62°×![]() =31°;
=31°;
(3)射线OD与OE之间的位置关系是:OD⊥OE,理由如下:
由(1)可知:∠DOE=∠COE+∠COD=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=90°,
∠AOB=90°,
∴OD⊥OE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于
 AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( ) 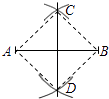
A.矩形
B.菱形
C.正方形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是线段
是线段 上一点,
上一点,  ,
,  .
.
(
 )
) __________
__________  ;
;(
 )动点
)动点 、
、 分别从
分别从 、
、 同时出发,点
同时出发,点 以
以 的速度沿
的速度沿 向右运动,终点为
向右运动,终点为 ;点
;点 以
以 的速度沿
的速度沿 向左运动,终点为
向左运动,终点为 .当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,
.当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,  、
、 、
、 三点,有一点恰好是以另两点为端点的线段的中点?
三点,有一点恰好是以另两点为端点的线段的中点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2
 ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用网格画图:
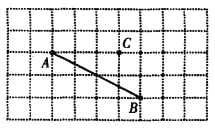
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系
 中,抛物线
中,抛物线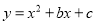 与
与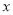 轴交于
轴交于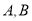 两点(点
两点(点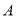 在点
在点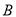 的左侧),与
的左侧),与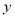 轴交于点
轴交于点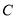 ,点
,点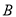 的坐标为
的坐标为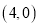 ,将直线
,将直线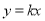 沿
沿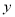 轴向上平移4个单位长度后恰好经过
轴向上平移4个单位长度后恰好经过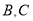 两点。
两点。(1)求直线
 及抛物线的解析式;
及抛物线的解析式;(2)将直线
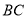 沿
沿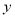 轴向上平移5个单位长度后与抛物线交于
轴向上平移5个单位长度后与抛物线交于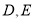 两点,若点
两点,若点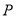 是抛物线位于直线
是抛物线位于直线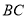 下方的一个动点,连接
下方的一个动点,连接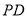 ,交直线
,交直线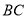 于点
于点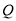 ,连接
,连接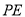 和
和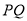 。设
。设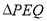 的面积为
的面积为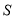 ,当S取得最大值时,求出此时点
,当S取得最大值时,求出此时点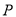 的坐标及
的坐标及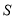 的最大值;
的最大值;(3)如图2,记(2)问中直线
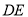 与
与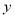 轴交于
轴交于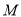 点,现有一点
点,现有一点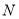 从
从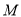 点出发,先沿
点出发,先沿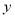 轴到达
轴到达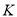 点,再沿
点,再沿 到达
到达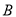 点,已知
点,已知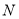 点在
点在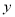 轴上运动的速度是每秒2个单位长度,它在直线
轴上运动的速度是每秒2个单位长度,它在直线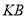 上运动速度是1个单位长度。现要使
上运动速度是1个单位长度。现要使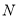 点按照上述要求到达
点按照上述要求到达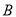 点所用的时间最短,请简述确定
点所用的时间最短,请简述确定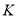 点位置的过程,求出点
点位置的过程,求出点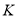 的坐标,不要求证明。
的坐标,不要求证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据某网站调查,2016年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其他共五类.根据调查的部分相关数据,绘制的统计图表如下:
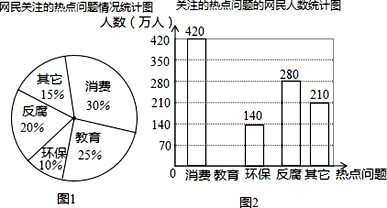
根据所给信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若成都市约有880万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
相关试题

