搜索
【题目】如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 
AB的长为半径画弧，两弧相交于C，D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（ ）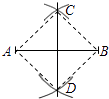 
A.矩形
B.菱形
C.正方形
D.等腰梯形
参考答案：
【答案】B
【解析】解：∵分别以A和B为圆心，大于 
AB的长为半径画弧，两弧相交于C、D， ∴AC=AD=BD=BC，
∴四边形ADBC一定是菱形，
故选：B．
【考点精析】关于本题考查的线段垂直平分线的性质和菱形的判定方法，需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能得出正确答案．
-
科目： 来源： 题型：
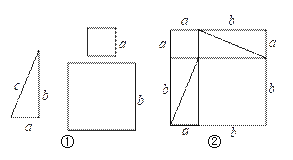
查看答案和解析>>【题目】如图①是1个直角三角形和2个小正方形，直角三角形的三条边长分别是a、b、c，其中a、b是直角边．2个小正方形的边长分别是a、b．
（1）将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②)．用两种不同的方法列代数式表示图②中的大正方形面积：方法一：_______；方法二：_____；
（2）观察图②，试写出(a+b)2，a2，2ab，b2这四个代数式之间的等量关系，为___ ____；
（3）利用你发现的结论，求：9922+16×992+64的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【探索新知】
如图1，点C将线段AB分成AC和BC两部分，若BC=
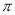AC，则称点C是线段AB的圆周率点，线段AC、BC称作互为圆周率伴侣线段.(1)若AC=3，则AB=_____；
(2)若点D也是图1中线段AB的圆周率点(不同于C点)，则AC_____DB；(填“=”或“≠”)
【深入研究】
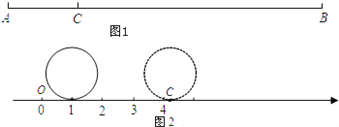
如图2，现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点，求线段MN的长度.
-
科目： 来源： 题型：
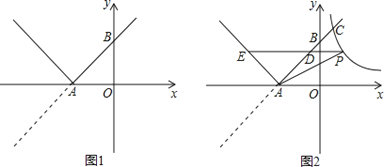
查看答案和解析>>【题目】如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）．
（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；
（2）如图2，双曲线y=与新函数的图象交于点C（1，a），点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．
①试求△PAD的面积的最大值；
②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
是线段
上一点， 
， 
．
（
）
__________ 
；（
）动点
、
分别从
、
同时出发，点
以
的速度沿
向右运动，终点为
；点
以
的速度沿
向左运动，终点为
．当一个点到达终点，另一个点也随之停止运动．求运动多少秒时， 
、
、
三点，有一点恰好是以另两点为端点的线段的中点？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，BA=BC，以AB为直径的⊙O分别交AC、BC于点D、E，BC的延长线于⊙O的切线AF交于点F．
（1）求证：∠ABC=2∠CAF；
（2）若AC=2
，CE：EB=1：4，求CE的长．
-
科目： 来源： 题型：
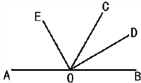
查看答案和解析>>【题目】如图，点O在直线AB上，OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____；∠BOD的余角是______；
(2)若∠AOC=118°，求∠COD的度数；
(3)射线OD与OE之间有什么特殊的位置关系？为什么？
相关试题
