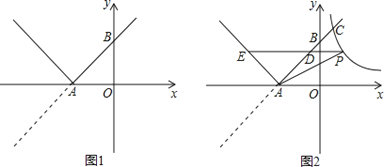
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
参考答案:
【答案】(1)①函数的最小值为0;②函数图象的对称轴为直线x=-3;新函数的解析式为y=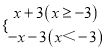 ;(2)△PAD的面积的最大值为
;(2)△PAD的面积的最大值为![]() ;②在点D运动的过程中,四边形PAEC不能为平行四边形.理由见解析.
;②在点D运动的过程中,四边形PAEC不能为平行四边形.理由见解析.
【解析】(1)根据一次函数的性质,结合函数图象可写出新函数的两条性质;求新函数的解析式,可分两种情况进行讨论:①x≥-3时,显然y=x+3;②当x<-3时,利用待定系数法求解;
(2)①先把点C(1,a)代入y=x+3,求出C(1,4),再利用待定系数法求出反比例函数解析式为y=![]() .由点D是线段AC上一动点(不包括端点),可设点D的坐标为(m,m+3),且-3<m<1,那么P(
.由点D是线段AC上一动点(不包括端点),可设点D的坐标为(m,m+3),且-3<m<1,那么P(![]() ,m+3),PD=
,m+3),PD=![]() -m,再根据三角形的面积公式得出△PAD的面积为S=
-m,再根据三角形的面积公式得出△PAD的面积为S=![]() (
(![]() -m)×(m+3)=-
-m)×(m+3)=-![]() m2-
m2-![]() m+2=-
m+2=-![]() (m+
(m+![]() )2+
)2+![]() ,然后利用二次函数的性质即可求解;
,然后利用二次函数的性质即可求解;
②先利用中点坐标公式求出AC的中点D的坐标,再计算DP,DE的长度,如果DP=DE,那么根据对角线互相平分的四边形是平行四边形可得四边形PAEC为平行四边形;如果DP≠DE,那么不是平行四边形.
试题解析:(1)如图1,均是正整数新函数的两条性质:①函数的最小值为0;
②函数图象的对称轴为直线x=-3;
由题意得A点坐标为(-3,0).分两种情况:
①x≥-3时,显然y=x+3;
②当x<-3时,设其解析式为y=kx+b.
在直线y=x+3中,当x=-4时,y=-1,
则点(-4,-1)关于x轴的对称点为(-4,1).
把(-4,1),(-3,0)代入y=kx+b,
得![]()
解得![]()
∴y=-x-3.
综上所述,新函数的解析式为y=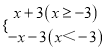 ;
;
(2)如图2,
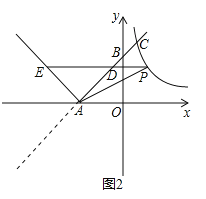
①∵点C(1,a)在直线y=x+3上,
∴a=1+3=4.
∵点C(1,4)在双曲线y=![]() 上,
上,
∴k=1×4=4,y=![]() .
.
∵点D是线段AC上一动点(不包括端点),
∴可设点D的坐标为(m,m+3),且-3<m<1.
∵DP∥x轴,且点P在双曲线上,
∴P(![]() ,m+3),
,m+3),
∴PD=![]() -m,
-m,
∴△PAD的面积为
S=![]() (
(![]() -m)×(m+3)=-
-m)×(m+3)=-![]() m2-
m2-![]() m+2=-
m+2=-![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵a=-![]() <0,
<0,
∴当m=-![]() 时,S有最大值,为
时,S有最大值,为![]() ,
,
又∵-3<-![]() <1,
<1,
∴△PAD的面积的最大值为![]() ;
;
②在点D运动的过程中,四边形PAEC不能为平行四边形.理由如下:
当点D为AC的中点时,其坐标为(-1,2),此时P点的坐标为(2,2),E点的坐标为(-5,2),
∵DP=3,DE=4,
∴EP与AC不能互相平分,
∴四边形PAEC不能为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于空气污染,气候干旱等因素,今年流感大肆流行,根据山东省卫计委统计,截止2018年1月,本年度全省共报告流感样病例442000例,其中0﹣14岁年龄组占到总病例数的88.09%,用科学记数法表示数字442000是( )
A. 4.42×103 B. 442×103 C. 4.42×105 D. 442×105
-
科目: 来源: 题型:
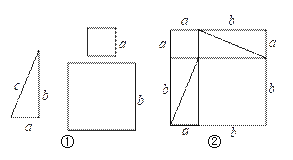
查看答案和解析>>【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边.2个小正方形的边长分别是a、b.
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:方法一:_______;方法二:_____;
(2)观察图②,试写出(a+b)2,a2,2ab,b2这四个代数式之间的等量关系,为___ ____;
(3)利用你发现的结论,求:9922+16×992+64的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探索新知】
如图1,点C将线段AB分成AC和BC两部分,若BC=
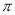 AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
AC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.(1)若AC=3,则AB=_____;
(2)若点D也是图1中线段AB的圆周率点(不同于C点),则AC_____DB;(填“=”或“≠”)
【深入研究】
如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N均为线段OC的圆周率点,求线段MN的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于
 AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( ) 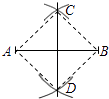
A.矩形
B.菱形
C.正方形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是线段
是线段 上一点,
上一点,  ,
,  .
.
(
 )
) __________
__________  ;
;(
 )动点
)动点 、
、 分别从
分别从 、
、 同时出发,点
同时出发,点 以
以 的速度沿
的速度沿 向右运动,终点为
向右运动,终点为 ;点
;点 以
以 的速度沿
的速度沿 向左运动,终点为
向左运动,终点为 .当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,
.当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,  、
、 、
、 三点,有一点恰好是以另两点为端点的线段的中点?
三点,有一点恰好是以另两点为端点的线段的中点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2
 ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
相关试题

