【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y![]() 轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.

(![]() )求抛物线的表达式.
)求抛物线的表达式.
(![]() )求一次函数
)求一次函数![]() 的表达式.
的表达式.
(![]() )将直线
)将直线![]() 绕其与
绕其与![]() 轴的交点
轴的交点![]() 旋转,使当
旋转,使当![]() 时,直线
时,直线![]() 总位于抛物线的下方,请结合函数图象,求
总位于抛物线的下方,请结合函数图象,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)y=x2-2x-1;(2)一次函数y=x+n的表达式是y=x-3;(3)当-5<m<1时,当-1≤x≤1时,直线l总位于抛物线的下方.
【解析】试题分析:(1)根据A和B对称,可求得对称轴,则b的值即可求得,然后根据函数经过点C(0,1).代入即可求得c的值,则抛物线解析式即可求得;
(2)首先求得抛物线的顶点,代入一次函数解析式即可求得n的值,求得一次函数的解析式;
(3)首先求得抛物线上当![]() 和
和![]() 时对应点的坐标,然后求得直线
时对应点的坐标,然后求得直线![]() 经过这两个点时对应的
经过这两个点时对应的![]() 的值,据此即可求解.
的值,据此即可求解.
试题解析:(1)二次函数的对称轴是![]()
则![]()
解得:b=2,
∵抛物线与y轴交于点C(0,1).
∴c=1,
则二次函数的解析式是![]() ;
;
(2)二次函数![]() 的顶点坐标是(1,2),
的顶点坐标是(1,2),
代入y=x+n得2=1+n,
解得:n=3,
则一次函数y=x+n的表达式是y=x3;
(3)如图所示:
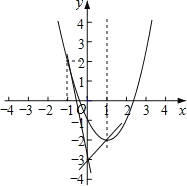
在![]() 中,当x=1时,y=2;
中,当x=1时,y=2;
当x=1时,y=2.
当直线y=mx3经过点(1,2)时,m3=2,解得:m=5;
当直线y=mx3经过点(1,2)时,m3=2,解得:m=1.
则当5<m<1时,当![]() 时,直线l总位于抛物线的下方.
时,直线l总位于抛物线的下方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,点E,F分别是边AD,CD上的两个动点,且满足AE+CF=BD=2,设△BEF的面积为S,则S的取值范围是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】准备两张同样大小的正方形纸片.
(1)取准备好的一张正方形纸片,将它的四周各剪去一个同样大小的正方形(如图1),再折合成一个无盖的长方体盒子.做成的长方体盒子的底面的边长为6cm,容积为108cm3,那么原正方形纸片的边长为多少?
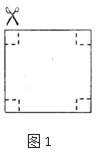
(2)取准备好的另一张一样的正方形纸片,这张纸片恰好可做成圆柱形食品罐侧面的包装纸(如图2,不计接口部分),求这个食品罐的底面圆的半径?(结果保留
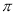 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:y=y1﹣y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时y=1.
(1)求y关于x的函数关系式.
(2)求x=﹣
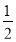 时,y的值.
时,y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 )探究发现
)探究发现下面是一道例题及其解答过程,请补充完整:
如图①在等边
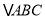 内部,有一点
内部,有一点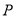 ,若
,若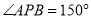 ,求证:
,求证: 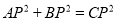 ,
,证明:将
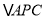 绕
绕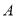 点逆时针旋转
点逆时针旋转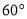 ,得到
,得到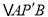 ,连接
,连接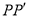 ,则
,则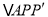 为等边三角形.
为等边三角形.∴
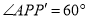 ,
, 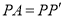 ,
, 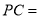 __________.
__________.∵
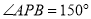 ,∴
,∴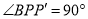 ,
,∴
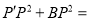 __________,
__________,即
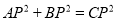 ,
,(
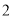 )类比延伸:
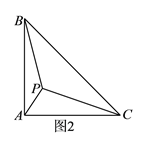
)类比延伸:如图②在等腰三角形
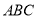 中,
中,  ,内部有一点
,内部有一点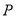 ,若
,若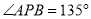 ,试判断线段
,试判断线段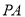 、
、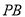 、
、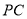 之间的数量关系,并证明.
之间的数量关系,并证明.(
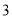 )联想拓展:
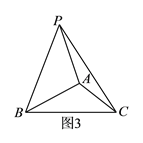
)联想拓展:如图③在
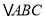 中,
中, 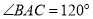 ,
, 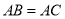 ,点
,点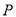 在直线
在直线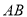 上方,且
上方,且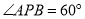 ,满足
,满足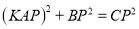 ,请直接写出
,请直接写出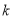 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
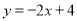 的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o,
的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o, 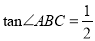 .
.(1)求点
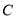 的坐标;
的坐标;(2)在第一象限内有一点M(1,m),且点M与点C位于直线AB的同侧,使得
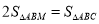 ,求点M的坐标.
,求点M的坐标.
相关试题

