【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
参考答案:
【答案】(1)有n张桌子时,第一种能坐(4n+2)人,第二种能坐(2n+4)人.
(2)选择第一种摆放方式,理由见解析.
【解析】试题分析:能够根据桌子的摆放发现规律,然后进行计算判断.
试题解析:解:(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人.
即有n张桌子时是6+4(n﹣1)=4n+2.
第二种中,有一张桌子是6人,后边多一张桌子多2人,
即6+2(n﹣1)=2n+4;
(2)打算用第一种摆放方式来摆放餐桌;
因为,当n=25时,4×25+2=102>98,
当n=25时,2×25+4=54<98,
所以,选用第一种摆放方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣
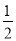 x2+
x2+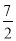 x+4经过A、B两点.
x+4经过A、B两点.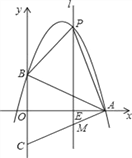
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(3,b)在第四象限内,则点Q(b,﹣3)所在象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,地球的体积约是太阳体积的倍数是( )
A.7.1×10﹣6
B.7.1×10﹣7
C.1.4×106
D.1.4×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的一次函数,且当x=﹣4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的解析式;
(2)当x=﹣ 时,函数y的值;
时,函数y的值;
(3)当y<1时,自变量x取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在不透明的袋子中装有2个黑球和3个红球,这些球只有颜色不同,随机从袋子中摸出三个球,下列事件是必然事件的是( )
A.摸出的三个球中至少有一个球是红球
B.摸出的三个球中至少有两个球是黑球
C.摸出的三个球中至少有一个球是黑球
D.摸出的三个球中至少有两个球是红球
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=2,a﹣b=﹣1,则代数式a2b﹣ab2的值等于 .
相关试题

