【题目】如图,菱形ABCD的边长为2,点E,F分别是边AD,CD上的两个动点,且满足AE+CF=BD=2,设△BEF的面积为S,则S的取值范围是______.

参考答案:
【答案】![]() ≤S≤
≤S≤![]() .
.
【解析】
先证明△BDE≌△BCF,再求出△BEF为正三角形即可解答.
解:∵菱形ABCD的边长为2,BD=2,
∴△ABD和△BCD都为正三角形,
∴∠BDE=∠BCF=60°,BD=BC,
∵AE+DE=AD=2,而AE+CF=2,
∴DE=CF,
∴△BDE≌△BCF(SAS);
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
设BE=BF=EF=x,
则S=![]() xxsin60°=
xxsin60°=![]() x2,
x2,
当BE⊥AD时,x最小=2×sin60°=![]() ,
,
∴S最小=![]() ×(
×(![]() )2=
)2=![]() ,
,
当BE与AB重合时,x最大=2,
∴S最大=![]() ×22=
×22=![]() ,
,
∴![]() ≤S≤
≤S≤![]() .
.
故答案为:![]() ≤S≤
≤S≤![]() .
.
-
科目: 来源: 题型:
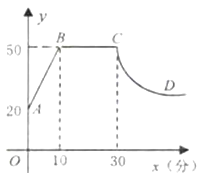
查看答案和解析>>【题目】心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中
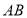 、
、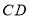 分别为线段,
分别为线段,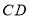 为双曲线的一部分)。
为双曲线的一部分)。(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知——自主探索,合作交流——总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40,请问这样的课堂学习安排是否合理?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 和函数
和函数 的图象之间的关系,小东根据学习函数的经验,通过画出两个函数图象后,再观察研究.
的图象之间的关系,小东根据学习函数的经验,通过画出两个函数图象后,再观察研究.下面是小东的探究过程,请补充完成:
(
 )下表是
)下表是 与
与 的几组对应值.
的几组对应值.
…










…

…











…
下表是
 与
与 的几组对应值
的几组对应值
…











…

…





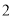





…
请补全表格
 __________.
__________.(
 )如下图,在平面直角坐标系
)如下图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点,请根据描出的点,在同一坐标系中画出
中,描出了以上表中各对对应值为坐标的点,请根据描出的点,在同一坐标系中画出 和函数
和函数 的图象.
的图象.
(
 )观察这两个函数的图象,发现这两个函数图象是关于直线成轴对称的,请画出这条直线.
)观察这两个函数的图象,发现这两个函数图象是关于直线成轴对称的,请画出这条直线.(
 )已知
)已知 ,借助函数图象比较
,借助函数图象比较 ,
,  ,
,  的大小(用“
的大小(用“ ”号连接).
”号连接). -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,反比例函数y=
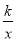 (x>0),过点A(3,4).
(x>0),过点A(3,4).(1)求y关于x的函数表达式.
(2)求当y≥2时,自变量x的取值范围.
(3)在x轴上有一点P(1,0),在反比例函数图象上有一个动点Q,以PQ为一边作一个正方形PQRS,当正方形PQRS有两个顶点在坐标轴上时,画出状态图并求出相应S点坐标.
-
科目: 来源: 题型:
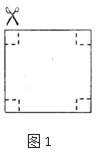
查看答案和解析>>【题目】准备两张同样大小的正方形纸片.
(1)取准备好的一张正方形纸片,将它的四周各剪去一个同样大小的正方形(如图1),再折合成一个无盖的长方体盒子.做成的长方体盒子的底面的边长为6cm,容积为108cm3,那么原正方形纸片的边长为多少?
(2)取准备好的另一张一样的正方形纸片,这张纸片恰好可做成圆柱形食品罐侧面的包装纸(如图2,不计接口部分),求这个食品罐的底面圆的半径?(结果保留
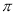 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:y=y1﹣y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时y=1.
(1)求y关于x的函数关系式.
(2)求x=﹣
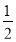 时,y的值.
时,y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y
 轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
(
 )求抛物线的表达式.
)求抛物线的表达式.(
 )求一次函数
)求一次函数 的表达式.
的表达式.(
 )将直线
)将直线 绕其与
绕其与 轴的交点
轴的交点 旋转,使当
旋转,使当 时,直线
时,直线 总位于抛物线的下方,请结合函数图象,求
总位于抛物线的下方,请结合函数图象,求 的取值范围.
的取值范围.
相关试题

