【题目】已知一次函数![]() 的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o,
的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o, ![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)在第一象限内有一点M(1,m),且点M与点C位于直线AB的同侧,使得![]() ,求点M的坐标.
,求点M的坐标.

参考答案:
【答案】(1)点C坐标是(4,1).(2)M(1, ![]() ).
).
【解析】试题分析:(1)先求出点A、点B的坐标,再求出AB的长,AC的长.
过C点作CD⊥![]() 轴于点D,易得△OBA∽△DAC,得出AD=2,CD=1,从而得到结论.
轴于点D,易得△OBA∽△DAC,得出AD=2,CD=1,从而得到结论.
(2)求出![]() =5,S△ABM =
=5,S△ABM =![]() ,ME=m-2,分别过点A、B作直线x=1的垂线,垂足分别是点F、G,得到AF+BG = OA = 2,由S△ABM = S△BME + S△AME =
,ME=m-2,分别过点A、B作直线x=1的垂线,垂足分别是点F、G,得到AF+BG = OA = 2,由S△ABM = S△BME + S△AME =![]() ,得到ME的长,从而得到结论.
,得到ME的长,从而得到结论.
试题解析:解:(1)令y=0,则-2x+4=0,解得:x=2,∴点A坐标是(2,0).
令x=0,则y=4,∴点B坐标是(0,4),∴AB=![]() =
=![]() =
=![]() .
.
∵∠BAC=90°,tan∠ABC=![]() ,∴AC=
,∴AC=![]() .
.
过C点作CD⊥![]() 轴于点D,易得△OBA∽△DAC,∴AD=2,CD=1,∴点C坐标是(4,1).
轴于点D,易得△OBA∽△DAC,∴AD=2,CD=1,∴点C坐标是(4,1).
(2)![]() =
=![]() ABAC=
ABAC=![]() =5.
=5.
∵2S△ABM=S△ABC,∴S△ABM =![]() .
.
∵M(1,m),∴点M在直线x=1上;
令直线x=1与线段AB交于点E,ME=m-2;
分别过点A、B作直线x=1的垂线,垂足分别是点F、G,∴AF+BG = OA = 2;
S△ABM = S△BME + S△AME =![]() MEBG+
MEBG+![]() MEAF=
MEAF=![]() ME(BG+AF)=
ME(BG+AF)=![]() MEOA=
MEOA=![]() ×2×ME=
×2×ME=![]() ,
,
∴ME=![]() ,m-2=
,m-2=![]() ,m=
,m=![]() ,∴M(1,
,∴M(1, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y
 轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
(
 )求抛物线的表达式.
)求抛物线的表达式.(
 )求一次函数
)求一次函数 的表达式.
的表达式.(
 )将直线
)将直线 绕其与
绕其与 轴的交点
轴的交点 旋转,使当
旋转,使当 时,直线
时,直线 总位于抛物线的下方,请结合函数图象,求
总位于抛物线的下方,请结合函数图象,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 )探究发现
)探究发现下面是一道例题及其解答过程,请补充完整:
如图①在等边
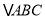 内部,有一点
内部,有一点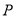 ,若
,若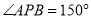 ,求证:
,求证: 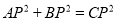 ,
,证明:将
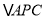 绕
绕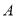 点逆时针旋转
点逆时针旋转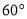 ,得到
,得到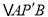 ,连接
,连接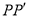 ,则
,则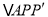 为等边三角形.
为等边三角形.∴
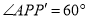 ,
, 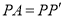 ,
, 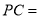 __________.
__________.∵
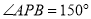 ,∴
,∴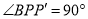 ,
,∴
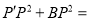 __________,
__________,即
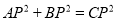 ,
,(
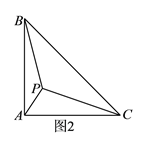
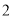 )类比延伸:
)类比延伸:如图②在等腰三角形
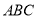 中,
中,  ,内部有一点
,内部有一点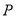 ,若
,若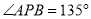 ,试判断线段
,试判断线段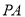 、
、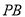 、
、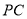 之间的数量关系,并证明.
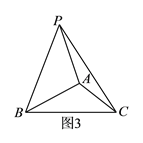
之间的数量关系,并证明.(
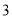 )联想拓展:
)联想拓展:如图③在
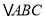 中,
中, 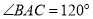 ,
, 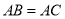 ,点
,点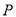 在直线
在直线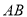 上方,且
上方,且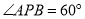 ,满足
,满足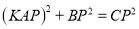 ,请直接写出
,请直接写出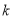 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
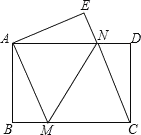
查看答案和解析>>【题目】如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,ND=1.
①求MC的长.
②求MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多
 小时,求自行车的平均速度?
小时,求自行车的平均速度? -
科目: 来源: 题型:
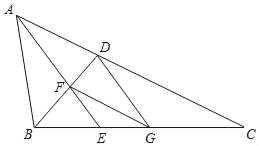
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
相关试题

