【题目】已知关于x的方程x2﹣(2k+1)x+4(k﹣ ![]() )=0
)=0
(1)求证:无论k取何值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.
参考答案:
【答案】
(1)证明:△=(2k+1)2﹣4×4(k﹣ ![]() )
)
=4k2+4k+1﹣16k+8,
=4k2﹣12k+9
=(2k﹣3)2,
∵(2k﹣3)2≥0,即△≥0,
∴无论k取何值,这个方程总有实数根;
(2)解:当b=c时,△=(2k﹣3)2=0,解得k= ![]() ,方程化为x2﹣4x+4=0,解得b=c=2,而2+2=4,故舍去;
,方程化为x2﹣4x+4=0,解得b=c=2,而2+2=4,故舍去;
当a=b=4或a=c=4时,把x=4代入方程得16﹣4(2k+1)+4(k﹣ ![]() )=0,解得k=
)=0,解得k= ![]() ,方程化为x2﹣6x+8=0,解得x1=4,x2=2,即a=b=4,c=2或a=c=4,b=2,
,方程化为x2﹣6x+8=0,解得x1=4,x2=2,即a=b=4,c=2或a=c=4,b=2,
所以△ABC的周长=4+4+2=10.
【解析】(1)先计算判别式的值得到△=4k2﹣12k+9,配方得到△=(2k﹣3)2 , 根据非负数的性质易得△≥0,则根据判别式的意义即可得到结论;(2)分类讨论:当b=c时,则△=(2k﹣3)2=0,解得k= ![]() ,然后解方程得到b=c=2,根据三角形三边关系可判断这种情况不符号条件;当a=b=4或a=c=4时,把x=4代入方程可解得k=
,然后解方程得到b=c=2,根据三角形三边关系可判断这种情况不符号条件;当a=b=4或a=c=4时,把x=4代入方程可解得k= ![]() ,则方程化为x2﹣6x+8=0,解得x1=4,x2=2,所以a=b=4,c=2或a=c=4,b=2,然后计算△ABC的周长.
,则方程化为x2﹣6x+8=0,解得x1=4,x2=2,所以a=b=4,c=2或a=c=4,b=2,然后计算△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2﹣4ac,M=(2ax1+b)2 , 则关于△与M大小关系的下列说法中,正确的是( )
A.△>M
B.△=M
C.△<M
D.无法确定△与M的大小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论: ①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ;
;
④ ≤n≤4.
≤n≤4.
其中正确的有( )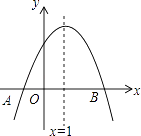
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求
 的值;
的值;若AD=3,则OE的长为_________(直接写出结果).


-
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
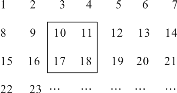
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
-
科目: 来源: 题型:
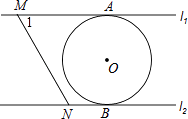
查看答案和解析>>【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 .
相关试题

