Question

【题目】如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论： ①当x=3时，y=0；
②3a+b＞0；
③﹣1≤a≤﹣ ；
④ ≤n≤4．
其中正确的有（ ）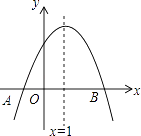

A.1个
B.2个
C.3个
D.4个

Answer 1

【答案】C
【解析】解：①由抛物线的对称性可知： 抛物线与x轴的另一交点横坐标为1×2﹣（﹣1）=3，
即点B的坐标为（3，0），
∴当x=3时，y=0，①正确；
②∵抛物线开口向下，
∴a＜0．
∵抛物线的顶点坐标为（1，n），
∴抛物线的对称轴为x=﹣ =1，
∴b=﹣2a，
3a+b=a＜0，②不正确；
③∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），
∴2≤c≤3．
令x=﹣1，则有a﹣b+c=0，
又∵b=﹣2a，
∴3a=﹣c，即﹣3≤3a≤﹣2，
解得：﹣1≤a≤﹣ ，③正确；
④∵抛物线的顶点坐标为（﹣ ， ），
∴n= =c﹣ ，
又∵b=﹣2a，2≤c≤3，﹣1≤a≤﹣ ，
∴n=c﹣a， ≤n≤4，④正确．
综上可知：正确的结论为①③④．
故选C．
【考点精析】根据题目的已知条件，利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．