【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


参考答案:
【答案】![]()
【解析】(1)过点B作BM∥FG交CD于M ,构造三角形,证△BCM≌△CDE,可得; CE=BM=FG;(2) 过点B作BM∥FG交CD于M , 连接MO,由(1)证BC=BO,再证MC=MO=MG=ED,又AD=3DE,所以![]() ;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
又BM=CE=![]() ,再根据面积公式得OC=2×
,再根据面积公式得OC=2×![]() .
.
(1)过点B作BM∥FG交CD于M ,
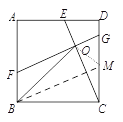
易证四边形FBMG为平行四边形
∴FG=BM,
由BC=CD;∠BCM=∠CDE;∠MBC=∠ECD
可证△BCM≌△CDE,
∴CE=BM=FG;
(2)过点B作BM∥FG交CD于M ,
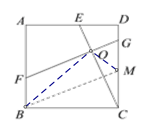
由(1)知△BCM≌△CDE,又∠OBC=2∠DCE ,
MC=ED,∠MBC=∠DCE=∠MBO,
由BM∥FG得MB⊥CE,
∴∠BOC=∠BCO,
∴BC=BO,连接MO,
∴BM垂直平分OC,
∴MC=MO,
又∵∠GOM=∠BMO=∠BMC=∠OGM
∴MC=MO=MG=ED,
又AD=3DE,
∴![]() ;
;
(3)∵AD=3,
∴由(1)(2)可得
DE=OM=1,BO=AD=3,∴BM=CE=![]() ,
,
OC=2×![]() =2×
=2×![]() =
= ![]() ,
, ![]()
![]()
∴OE=CE-CO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论: ①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ;
;
④ ≤n≤4.
≤n≤4.
其中正确的有( )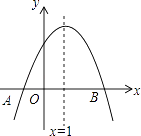
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k+1)x+4(k﹣
 )=0
)=0
(1)求证:无论k取何值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
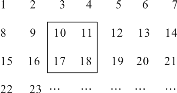
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 .
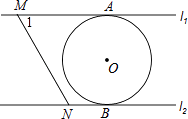
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数分别为_____和_____,p的值为_____.若以C为原点,p的值为_____;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p;
(3)若原点O在图中数轴上点C的右边,且CO=a,求p(用含a的代数式表示).
(4)若原点O在图中数轴上线段BC上,且CO=a,求p(用含a的代数式表示).利用此结果计算当a=0.5时,p的值.
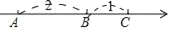
相关试题

