【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.

(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
参考答案:
【答案】(1)证明见解析;(2)90°;(3)![]() .
.
【解析】
(1)先证明△ADC≌△EDB,可得∠CAD=∠BED,进而可得结论;
(2)由勾股定理逆定理可得△ABE是直角三角形,∠E=90°,进而可得∠CAD=∠E=90°;
(3)先由勾股定理求CD,再由AFCD=ACAD可求AF即可.
解:(1)证明:∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,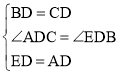 ,
,
∴△ADC≌△EDB(SAS),
∴∠CAD=∠BED,
∴BE∥AC.
(2)∵△ADC≌△EDB,
∴BE=AC=5,
在△ABE中,∵AB=13,BE=5,AE=2AD=12,
∴AE2+BE2=122+52=169,AB2=132=169,
∴AE2+BE2=AB2
∴∠E=90°,
∵BE∥AC,
∴∠CAD=∠E=90°;
(3)如图,过点A作AF⊥BC于F,
在Rt△ACD中,CD=![]() =
=![]() =
=![]() ,
,
∵AFCD=ACAD,
∴AF=![]() =
=![]() =
=![]() ,
,
即点A到BC的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>﹣1;④关于x的方程ax2+bx+c=0有一个根为﹣
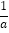 ,其中正确的结论个数是( )
,其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
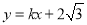 与
与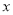 轴、
轴、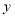 轴分别相交于点
轴分别相交于点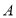 、点
、点 ,
,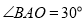 ,若将
,若将 沿直线
沿直线 折叠,使点
折叠,使点 与点
与点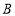 重合,折痕
重合,折痕 与
与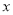 轴交于点
轴交于点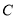 ,与
,与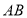 交于点
交于点 .
.(1)求
 的值;
的值;(2)求点
 的坐标;
的坐标;(3)求直线
 的表达式.
的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A旋转后得到△ACE,连接DE交AC于点F,则△AEF的面积为_______.

-
科目: 来源: 题型:
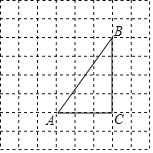
查看答案和解析>>【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
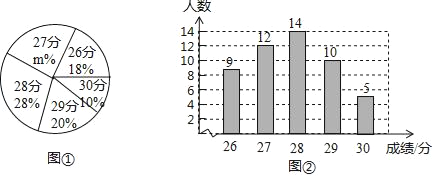
(1)本次随机抽样调查的学生人数为______,图①中的m的值为______;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校九年级共有学生300人,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作
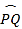 ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交
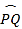 于点M,N;
于点M,N;(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
相关试题

