【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点
、点![]() ,
,![]() ,若将
,若将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的表达式.
的表达式.

参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() ; (3)
; (3)![]()
【解析】
(1)先求得点B的坐标,得到![]() 2
2![]() ,再根据
,再根据![]() 角所对直角边等于斜边一半结合勾股定理即可求得
角所对直角边等于斜边一半结合勾股定理即可求得![]() 的长,从而求得答案;
的长,从而求得答案;
(2)根据折叠的性质可证得BC=AC,设![]() ,则
,则![]() ,在
,在![]() 中,利用勾股定理即可求得答案;
中,利用勾股定理即可求得答案;
(3)点D时AB的中点,则点D(3,![]() ),将点C、D的坐标代入一次函数表达式,即可求解.
),将点C、D的坐标代入一次函数表达式,即可求解.
(1)令![]() ,则
,则![]() ,即:
,即:![]() 2
2![]() ,
,
∵![]() ,
,
∴![]() 4
4![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ;
;
(2)根据折叠的性质得:![]() ,
,
设![]() ,则
,则![]() ,
,
∴在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,则
,则![]() ,
,
则点C的坐标为:![]() ;
;
(3)根据折叠的性质知:点D是AB的中点,则点D的坐标为![]() ,
,
将点C、D的坐标代入一次函数的解析式![]() 得:
得: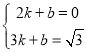 ,
,
解得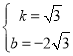 ,
,
故直线CD的表达式为:![]() .
.
-
科目: 来源: 题型:
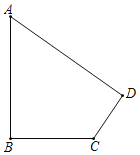
查看答案和解析>>【题目】如图,已知一块四边形的草地ABCD,其中∠B=90°,AB=20m,BC=15m,CD=7m,DA=24m,求这块草地的面积.
-
科目: 来源: 题型:
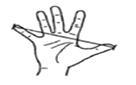
查看答案和解析>>【题目】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.人体构造学的研究成果表明,一般情况下人的指距
 和身高
和身高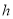 成如下所示的关系.
成如下所示的关系.
(1)直接写出身高
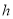 与指距
与指距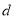 的函数关系式: .
的函数关系式: .(2)姚明的身高是226厘米,可预测他的指距约为多少?(精确到0.1厘米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>﹣1;④关于x的方程ax2+bx+c=0有一个根为﹣
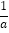 ,其中正确的结论个数是( )
,其中正确的结论个数是( )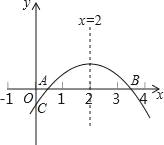
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A旋转后得到△ACE,连接DE交AC于点F,则△AEF的面积为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.

(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
-
科目: 来源: 题型:
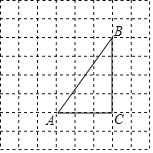
查看答案和解析>>【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
相关试题

