【题目】为了了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
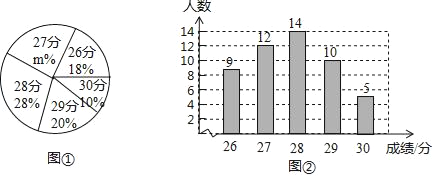
(1)本次随机抽样调查的学生人数为______,图①中的m的值为______;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校九年级共有学生300人,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.
参考答案:
【答案】(1) 50,24;(2)28,28,27.8;(3)174.
【解析】
(1)结合条形统计图和扇形统计图知:30分的人数为5人,占被调查人数的10%,用除法即可计算总人数,27分有12人,从而求出m;
(2)根据众数、中位数和平均数的概念计算即可;
(3) 根据题意,可知优秀的即是达28、29、30的人,共占58%,再进一步结合总体人数计算即可.
(1)本次随机抽样调查的学生人数为5÷10%=50;
12÷50=24%,即m=24.
(2)∵数据中28出现的次数最多,
∴本次抽样调查获取的样本数据的众数为28,
∵排序后,处于最中间的两个数为28和28,
∴中位数为(28+28)÷2=28,
x=![]() (9×26+12×27+14×28+10×29+5×30)=27.8,
(9×26+12×27+14×28+10×29+5×30)=27.8,
∴平均数为27.8;
(3)该校九年级学生体育成绩达到优秀的人数约为300×(28%+20%+10%)=174(人).
故答案为:(1) 50,24;(2)28,28,27.8;(3)174.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A旋转后得到△ACE,连接DE交AC于点F,则△AEF的面积为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.

(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
-
科目: 来源: 题型:
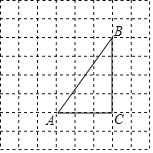
查看答案和解析>>【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作
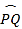 ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交
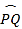 于点M,N;
于点M,N;(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是学习“分式方程应用”时,老师板书的例题和两名同学所列的方程.
15.3分式方程
例:有甲、乙两个工程队,甲队修路
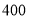 米与乙队修路
米与乙队修路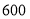 米所用时间相等.乙队每天比甲队多修
米所用时间相等.乙队每天比甲队多修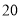 米,求甲队每天修路的长度.
米,求甲队每天修路的长度.冰冰:
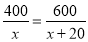
庆庆:
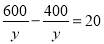
根据以上信息,解答下列问题:
(1)冰冰同学所列方程中的
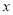 表示_____,庆庆同学所列方 程中的
表示_____,庆庆同学所列方 程中的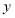 表示;
表示;(2)两个方程中任选一个,写出它的等量关系;
(3)解(2)中你所选择的方程,并解答老师的例题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,李老师让同学们试着用角尺平分
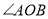 (如图所示),有两组.
(如图所示),有两组.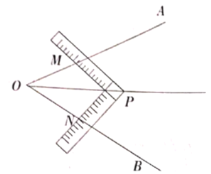
同学设计了如下方案:
方案①:将角尺的直角顶点
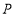 介于射线
介于射线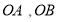 之间,移动角尺使角尺两边相同的刻度位于
之间,移动角尺使角尺两边相同的刻度位于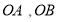 上,且交点分别为
上,且交点分别为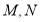 ,即
,即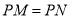 ,过角尺顶点
,过角尺顶点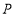 的射线
的射线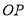 就是
就是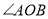 的平分线.
的平分线.方案②:在边
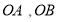 上分别截取
上分别截取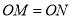 ,将角尺的直角顶点
,将角尺的直角顶点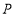 介于射线
介于射线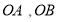 之间,移动角尺使角尺两边相同的刻度与点
之间,移动角尺使角尺两边相同的刻度与点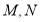 重合,即
重合,即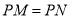 ,过角尺顶点
,过角尺顶点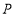 的射线
的射线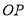 就是
就是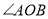 的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
相关试题

