搜索
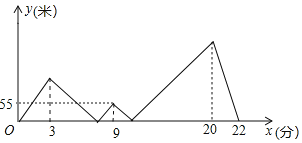
【题目】小明和父亲在一直线公路AB上进行（A→B→A）往返跑训练，两人同时从A点出发，父亲以较快的速度匀速跑到点B休息2分钟后立即原速跑回A点，小明先匀速慢跑了3分钟后，把速度提高到原来的
倍，又经过6分钟后超越了父亲一段距离，小明又将速度降低到出发时的速度，并以这一速度匀速跑到B点看到休息的父亲，然后立即以出发时的速度跑回A点，若两人之间的距离记为y（米），小明的跑步时间记为x（分），y和x的部分函数关系如图所示，则当父亲回到A点时小明距A点______米．
参考答案：
【答案】
【解析】
设父亲的速度为m米/分，小明的速度为n米/分，观察函数图象可知：父亲20分钟到达B地、小明22分钟到达B地、小明9分钟时比父亲多跑了55米，由此即可得出关于m、n的二元一次方程组，解之即可得出m、n的值，再由父亲往返的速度不变可知父亲返回A地需要20分钟，将m、n的值代入20m-20n中即可得出结论．
设父亲的速度为m米/分，小明的速度为n米/分，
根据题意得：
，
解得
，
∴20m-20n=，
答：当小亮回到A点时小花距A点米．
故答案为：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是正方形，其中A（
，
），B（
，），C（，
），将这个正方形向左平移3个单位长度，再向上平移1个单位长度，得正方形
． 
（1）画出平移后的正方形
； （2）写出点D和点D′ 的坐标；
（3）写出线段
与
的位置和大小关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．
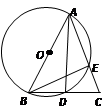
（1）D是BC的中点；
（2）△BEC∽△ADC；
（3）若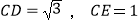
，求⊙O的半径。 -
科目： 来源： 题型：
查看答案和解析>>【题目】七年级320名学生参加安全知识竞赛活动，小明随机调查了部分学生的成绩（分数为整数），绘制了频率分布表和频数分布直方图（不完整），请结合图表信息回答下列问题：
成绩（分）
频数
71≤x＜76
2
76≤x＜81
8
81≤x＜86
12
86≤x＜91
10
91≤x＜96
6
96≤x＜101
2
（1）补全频数直方图；
（2）小明调查的学生人数是_______；频率分布表的组距是_______；
（3）七年级参加本次竞赛活动，分数
在
范围内的学生约有多少人． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）填空，并在括号内标注理由．
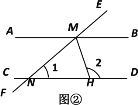
已知：如图①，DE∥BC，∠2=∠B，求证∠B+∠BFE=180°．
证明：∵DE
BC（已知），∴∠1=∠ （ ）．
又∵∠2=∠B（ 已知 ），∴∠ =∠ ．
∴ EF
（ ）． ∴∠B+∠BFE=180°（ ）．
（2）如图②，AB
CD，EF与AB，CD分别相交于点M，N，MH平分∠BMN，与CD相交于点H． 若∠1=40° ，求∠2的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市计划在城区投放一批“共享单车”，这批单车分为A，B两种不同款型，其中A型车单价400元，B型车单价320元．
（1）在“共享单车”试点，投放A，B两种款型的单车共100辆，总价值36 800元．试问本次试点投放的A型车与B型车各多少辆？
设本次试点投放的A型车
辆、B型车
辆．根据题意，列方程组___________
解这个方程组，得___________
答： ．
（2）该市决定在整个城区投放 “共享单车”．按照（Ⅰ）中试点投放A，B两车型的数量比进行投放，且投资总价值不低于184万元．请问整个城区投放的A型车至少多少辆？
-
科目： 来源： 题型：
查看答案和解析>>【题目】初202l届数学组的老师们为了拍摄《燃烧我的数学》的MTV，从全年级选了m人（m＞200）进行队列变换，现把m人排成一个10排的矩形队列，每排人数相等，然后把这个矩形队列平均分成A、B两个队列，如果从A队列中抽调36人到B队列，这样A、B队列都可以形成一个正方形队列，则m的值为______．
相关试题
