【题目】七年级320名学生参加安全知识竞赛活动,小明随机调查了部分学生的成绩(分数为整数),绘制了频率分布表和频数分布直方图(不完整),请结合图表信息回答下列问题:
成绩(分) | 频数 |
71≤x<76 | 2 |
76≤x<81 | 8 |
81≤x<86 | 12 |
86≤x<91 | 10 |
91≤x<96 | 6 |
96≤x<101 | 2 |

(1)补全频数直方图;
(2)小明调查的学生人数是_______;频率分布表的组距是_______;
(3)七年级参加本次竞赛活动,分数![]() 在
在![]() 范围内的学生约有多少人.
范围内的学生约有多少人.
参考答案:
【答案】(1)见解析;(2)40,5;(3)128人
【解析】
(1)根据频数分布表即可得出91≤x<96的人数为6人,由此可补全频数分布表;
(2)根据频数分布表将所有分数段的人数加在一起即可得调查的学生人数,求出每个小组的两个端点的距离即可求出组距;
(3)用总人数乘以分数在![]() 的人数所占比例即可得出分数
的人数所占比例即可得出分数![]() 在
在![]() 范围内的学生大致人数.
范围内的学生大致人数.
解:(1)补全频数直方图如下

(2)本次调查的学生人数为:2+8+12+10+6+2=40人,
频率分布表的组距是:76-71=5,
故答案为:40,5;
(3)![]() ,
,
∴分数![]() 在
在![]() 范围内的学生约有128人.
范围内的学生约有128人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题: (1)在被调查的学生中,喜欢“动画”节目的学生有 _____(名); (2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____(度).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,其中A(
 ,
, ),B(
),B( ,
, ),C(
),C( ,
, ),将这个正方形向左平移3个单位长度,再向上平移1个单位长度,得正方形
),将这个正方形向左平移3个单位长度,再向上平移1个单位长度,得正方形 .
. 
(1)画出平移后的正方形
 ;
; (2)写出点D和点D′ 的坐标;
(3)写出线段
 与
与 的位置和大小关系.
的位置和大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
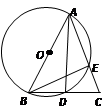
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若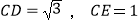 ,求⊙O的半径。
,求⊙O的半径。 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和父亲在一直线公路AB上进行(A→B→A)往返跑训练,两人同时从A点出发,父亲以较快的速度匀速跑到点B休息2分钟后立即原速跑回A点,小明先匀速慢跑了3分钟后,把速度提高到原来的
 倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠2=∠B,求证∠B+∠BFE=180°.
证明:∵DE
 BC(已知),
BC(已知),∴∠1=∠ ( ).
又∵∠2=∠B( 已知 ),∴∠ =∠ .
∴ EF
 ( ).
( ). ∴∠B+∠BFE=180°( ).
(2)如图②,AB
 CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
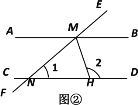
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市计划在城区投放一批“共享单车”,这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)在“共享单车”试点,投放A,B两种款型的单车共100辆,总价值36 800元.试问本次试点投放的A型车与B型车各多少辆?
设本次试点投放的A型车
 辆、B型车
辆、B型车 辆.
辆.根据题意,列方程组___________
解这个方程组,得___________
答: .
(2)该市决定在整个城区投放 “共享单车”.按照(Ⅰ)中试点投放A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问整个城区投放的A型车至少多少辆?
相关试题

