【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.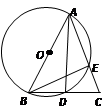
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
参考答案:
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90° 即AD是底边BC上的高.
又∵AB=AC,
∴△ABC是等腰三角形,
∴D是BC的中点
(2)证明:∵∠CBE与∠CAD是同弧所对的圆周角,
∴ ∠CBE=∠CAD.
又∵∠BCE=∠ACD,
∴△BEC∽△ADC;
(3)证明:由△BEC∽△ADC得: ![]() , 即CD·BC=AC·CE.
, 即CD·BC=AC·CE.
∵D是BC的中点,
∴CD= BC.
又∵AB=AC,∴CD·BC=AC·CE= ![]() BC ·BC=AB·CE 即BC
BC ·BC=AB·CE 即BC ![]() =2AB·CE=12
=2AB·CE=12
∴AB=6
∴⊙O的半径为3
【解析】(1)由AB是⊙O的直径,证出AD是底边BC上的高.根据等腰三角形三线合一的性质得出结论。
(2)根据同弧所对的圆周角相等,得出∠CBE=∠CAD,再根据两组角对应相等的两三角形相似。
(3)由△BEC∽△ADC得出对应边成比例,即可求出圆的半径。
【考点精析】本题主要考查了等腰三角形的性质和圆周角定理的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第8个图形中,十字星与五角星的个数和为( )

A. 25B. 27C. 28D. 31
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题: (1)在被调查的学生中,喜欢“动画”节目的学生有 _____(名); (2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____(度).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,其中A(
 ,
, ),B(
),B( ,
, ),C(
),C( ,
, ),将这个正方形向左平移3个单位长度,再向上平移1个单位长度,得正方形
),将这个正方形向左平移3个单位长度,再向上平移1个单位长度,得正方形 .
. 
(1)画出平移后的正方形
 ;
; (2)写出点D和点D′ 的坐标;
(3)写出线段
 与
与 的位置和大小关系.
的位置和大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级320名学生参加安全知识竞赛活动,小明随机调查了部分学生的成绩(分数为整数),绘制了频率分布表和频数分布直方图(不完整),请结合图表信息回答下列问题:
成绩(分)
频数
71≤x<76
2
76≤x<81
8
81≤x<86
12
86≤x<91
10
91≤x<96
6
96≤x<101
2

(1)补全频数直方图;
(2)小明调查的学生人数是_______;频率分布表的组距是_______;
(3)七年级参加本次竞赛活动,分数
 在
在 范围内的学生约有多少人.
范围内的学生约有多少人. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和父亲在一直线公路AB上进行(A→B→A)往返跑训练,两人同时从A点出发,父亲以较快的速度匀速跑到点B休息2分钟后立即原速跑回A点,小明先匀速慢跑了3分钟后,把速度提高到原来的
 倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.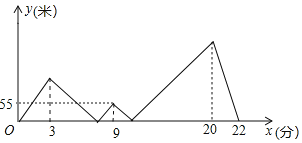
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠2=∠B,求证∠B+∠BFE=180°.
证明:∵DE
 BC(已知),
BC(已知),∴∠1=∠ ( ).
又∵∠2=∠B( 已知 ),∴∠ =∠ .
∴ EF
 ( ).
( ). ∴∠B+∠BFE=180°( ).
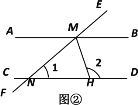
(2)如图②,AB
 CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
相关试题

