【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】
(1)①首先证明△ABA1是等边三角形,可得∠AA1B=∠A1BD1=60°,即可解决问题.
②首先证明△OCD1≌△OBA(AAS),推出OC=OB,再证明△DCO≌△ABO(SAS)即可解决问题.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.利用勾股定理求出AE,A1E即可解决问题.
(1)证明:①如图1中,
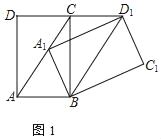
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
②如图2中,连接BD1.
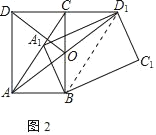
∵四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.
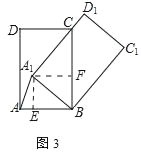
在Rt△A1BC中,∵∠CA1B=90°,BC=5.AB=3,
∴CA1=![]() =4,
=4,
∵![]() A1CA1B=
A1CA1B=![]() BCA1F,
BCA1F,
∴A1F=![]() ,
,
∵∠A1FB=∠A1EB=∠EBF=90°,
∴四边形A1EBF是矩形,
∴EB=A1F=![]() ,A1E=BF=
,A1E=BF=![]() ,
,
∴AE=3﹣![]() =
=![]() ,
,
在Rt△AA1E中,AA1=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处. 已知折痕AE=
 cm,且tan∠EFC=
cm,且tan∠EFC=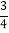 ,则矩形ABCD的周长为______cm.
,则矩形ABCD的周长为______cm.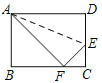
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得7条折痕,那么对折四次可以得到 条折痕,如果对折
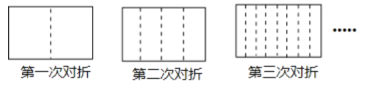 次,可以得到 条折痕.
次,可以得到 条折痕.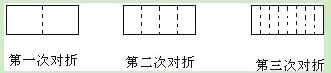
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
(3)借助(2)的思考过程与几何模型,直接写出代数式
 的最小值为 .
的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的
座位数
第2排的
座位数
第3排的
座位数
第4排的
座位数
…
a
a+2
a+4
…
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
-
科目: 来源: 题型:
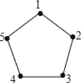
查看答案和解析>>【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了3km,到达小刚家,继续向东走了4km到达小红家,又向西走了11km到达小英家,最后回到超市。
(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴。并在数轴上表示出小刚家、小红家、小英家的位置;
(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米?
相关试题

