【题目】一辆货车从超市出发,向东走了3km,到达小刚家,继续向东走了4km到达小红家,又向西走了11km到达小英家,最后回到超市。
(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴。并在数轴上表示出小刚家、小红家、小英家的位置;
(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米?
参考答案:
【答案】(1)见解析;(2)7千米;(3)22千米;
【解析】
(1)以超市为原点,以向东方向为正方向,用1个单位长度表示1km,依此画出数轴,并在数轴上表示出小刚家、小红家、小英家的位置;
(2)根据已知图象可得;
(3)注意用绝对值来表示所走的总路程,再乘以耗油量可得答案.
(1)如图所示:

(2)由图知小英家距小刚家的距离为7km;
(3)货车一共行驶了3+4+11+4=22(km).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料,完成下列问题.
(1)我们已经学过了乘方运算,我们知道表示2个-2相乘,即
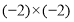 ,那么
,那么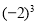 表示 ,把
表示 ,把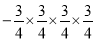 写成乘方的形式表示为 ,此时底数是 .
写成乘方的形式表示为 ,此时底数是 .(2)将(1)中两个底数同为-2的幂相乘,即
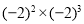 ,结果共有 个-2相乘,写成幂的形式为 ;
,结果共有 个-2相乘,写成幂的形式为 ;(3)若将(2)中算式中的底数都换为
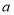 ,则
,则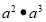 表示 ,计算结果为 .
表示 ,计算结果为 .若将(2)中算式中的指数换为正整数
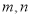 ,则
,则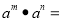 ,请用一句话概括你发现的结论 ;
,请用一句话概括你发现的结论 ;(4)利用上述结论,完成以下填空
若
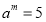 ,则
,则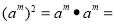 ,
,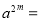 ;
;若
 ,
,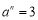 ,
,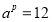 ,写出
,写出 的数量关系 .
的数量关系 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O(0,0),A(2,1),抛物线
 :
:  (h为常数)与y轴的交点为B.
(h为常数)与y轴的交点为B.(1)若t经过点A,求它的解析式,并写出此时t的对称轴及顶点坐标;
(2)设点B的纵坐标
 ,求
,求 的最大值,此时
的最大值,此时 上有两点(
上有两点( ),(
),( ),其中
),其中 >
> ,比较
,比较 与
与 的大.
的大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课堂探究性活动蔚然成风。张老师在课堂上设置一道习题:
(1)已知矩形ABCD和点P,当点P在BC上任一位置(如图1所示)时,探究PA2、PB2、PC2、PD2,之间的关系?直接写出结论,不必证明;
当P点在其它位置时,请同学们分组探究:
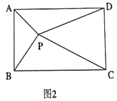
(2)当点P在矩形内部,如图2时,探究PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论写出来,并给予证明。
(3)当点P在矩形外部,如图3时,继续探完PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论直接写出来,不必证明。


-
科目: 来源: 题型:
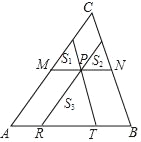
查看答案和解析>>【题目】如图,已知P为△ABC内一点,过P点分别作直线平行于△ABC的各边,形成小三角形的面积S1、S2、S3,分别为4、9、49,则△ABC的面积为_____.
相关试题

