【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
参考答案:
【答案】(1)a+6;(2)a+2(n-1);(3)38,510.
【解析】
试题分析:(1)第四排的座位数是第三排的座位数加上2,即可求解;(2)第n排的座位数比第一排多n-1个2,据此即可求解;(3)把a=20,n=10代入(2)中表达式即可求出第10排的座位数,当a=20时,利用梯形面积公式,上底为20,下底为a+2n-2=48,高为15,计算出面积即可求出容纳多少学生.
试题解析:(1)a+6;
(2)a+2(n-1);
(3)当a=20,n=10时,代入a+2(n-1)得,20+2×(10-1)=38;当a=20,n=15时,a+2n-2=20+30-2=48,
∴15排可容纳学生为![]() ×(20+48)×15=510(名)答:最多可容纳510名学生.
×(20+48)×15=510(名)答:最多可容纳510名学生.
-
科目: 来源: 题型:
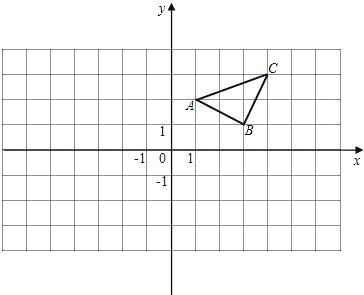
查看答案和解析>>【题目】(1)画出△ABC关于y轴的对称图形
 ,并写出
,并写出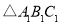 的顶点坐标;
的顶点坐标;(2)在x轴上求作点P,使PA+PC的值最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个附有进水管、出水管的水池,每单位时间内进出水管的进、出水量都是一定的,设从某时刻开始,4h内只进水不出水,在随后的时间内不进水只出水,得到的时间x(h)与水量y(m3)之间的关系图(如图).回答下列问题:
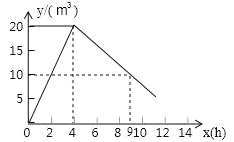
(1)进水管4h共进水多少?每小时进水多少?
(2)当0≤x≤4时,y与x有何关系?
(3)当x=9时,水池中的水量是多少?
(4)若4h后,只放水不进水,那么多少小时可将水池中的水放完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,BD是AC边上的中线,延长BC到E,使CE=CD.
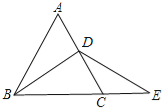
问:
(1)DB与DE相等吗?
(2)把BD是AC边上的中线改成什么条件,还能得到同样的结论?
-
科目: 来源: 题型:
查看答案和解析>>【题目】本市出租车的收费标准为:3千米以内(含3千米)收费5元,超过3千米的部分每千米收费1.20元(不足1千米按1千米计算),另加收0.60元的返空费.
(1)设行驶路程为x千米(
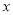 ≥3且取整数),用x表示出应收费y元的代数式;
≥3且取整数),用x表示出应收费y元的代数式;(2)当收费为10.40元时,该车行驶路程不超过多少千米?路程数在哪个范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次降价30%,标出“破产价”;第三次降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数
一
二
三
销售件数
10
40
一抢而光
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?
相关试题

